イメージベース構造解析ソフトウェア
VOXELCON
事例7 多孔質体の等価浸透係数およびミクロ流速分布
■概要
複合材料や多孔質材料などの利用増加にともない、これらのミクロ構造の特性を評価することの重要性が高まっています。
本例題では、VOXELCONの均質化法によるミクロ構造の流れ特性の評価の例として、多孔質体の等価浸透係数とミクロ流速分布の算出を紹介します。
■解析例1
解析モデル
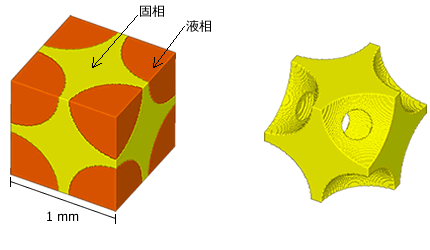
図のような周期構造をもつ多孔質体の等価浸透係数を算出します。
全体から1周期分のミクロ構造（ユニットセル）を抽出し、モデル化します。
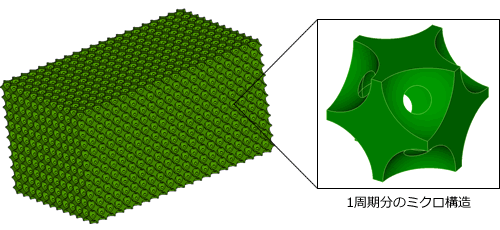
液相と固相をボクセルモデル化し、VOXELCONにより均質化解析を行います。
解析結果
等価浸透係数
均質化解析により得られた等価浸透係数は以下の通りです。
等方的な構造であるため、得られる等価浸透係数も等方性になっていることがわかります。
| X | Y | Z | |
|---|---|---|---|
| X | 1.237E-3 | -1.505E-9 | -2.124E-9 |
| Y | 1.237E-3 | -2.124E-9 | |
| Z | sym. | 1.237E-3 |
ここで得られる等価浸透係数は、流体の粘性によらず、ミクロ構造の大きさと形状にのみ依存する物性値です。
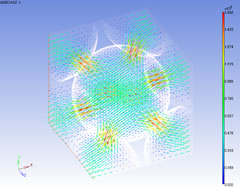
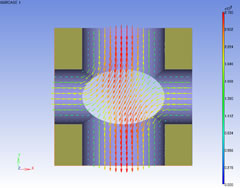
ミクロ流速分布
マクロ圧力勾配を以下のように仮定したときのミクロ構造内の流速分布を計算します。（単位：Pa/m）
| 圧力勾配 X | 圧力勾配 Y | 圧力勾配 Z | |
|---|---|---|---|
| パターン1 | 1.5×104 | 0 | 0 |
| パターン2 | 1.0×104 | 1.0×104 | 0 |
※粘性係数：0.9×10-3(Pa・s)
-
流速分布(mm/s)：パターン1
-
流速分布(mm/s)：パターン2
■解析例2
解析モデル
Y方向のみ流路の太いモデルの等価浸透係数を求めます。
-
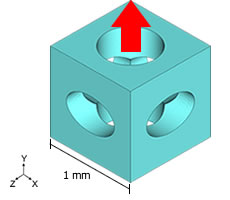
1周期分のミクロ構造
-
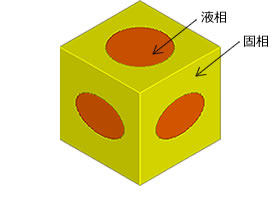
ボクセルモデル
解析結果
等価浸透係数
均質化解析により得られた等価浸透係数は以下の通りです。
Y方向のみ、他の方向より大きな浸透係数が得られていることがわります。
| X | Y | Z | |
|---|---|---|---|
| X | 1.782E-3 | 1.096E-7 | 1.486E-8 |
| Y | 3.503E-3 | 5.502E-8 | |
| Z | sym. | 1.782E-3 |
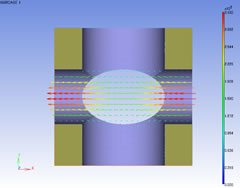
ミクロ流速分布
解析例1と同じマクロ圧力勾配を与えてミクロ流速分布を計算します。
-
流速分布(mm/s)：パターン1
-
流速分布(mm/s)：パターン2
■考察
均質化解析により、周期構造の1周期分のモデルから等価浸透係数を求めました。
またさらに、マクロ圧力勾配を仮定して、ミクロ構造内の流速分布を求めました。
本例では、マクロ圧力勾配を既知としましたが、得られた等価浸透係数を用いてマクロ浸透流解析を行い、その結果として得られるマクロ圧力勾配を利用することもできます。
このような多孔質体の例の他にも、RTM流動成形プロセスの解析など、"ミクロスケールにおける微細な空隙を通り道とする粘性流れ" と "マクロスケールにおけるダルシー則"を関係付けてマルチスケール解析を行いたい場合に、均質化法が有効です。
お問い合わせ
気になる点やご不明な点等、お気軽にお問い合わせください。
株式会社くいんと 営業本部 Tel 042(362)3884
