第20話 H1勾配法における製造制約
今回はOPTISHAPE-TSのノンパラメトリック形状最適化における製造制約の理論についてご紹介します。
*****
まずはじめに製造制約について簡単に説明しておきます。 形状最適化をはじめとしたノンパラメトリックな最適化はパラメトリックな最適化と比べて非常に自由度の高い手法となっていますが、それゆえに得られる形状もユニークなものとなります。 特に設定をしなければすべての領域が設計対象となり、評価関数の感度に従って自由に形を変えるので、最適化してみたはいいものの「この部分がこんなに変わっちゃったら他の部品と干渉しちゃうんだけど・・・」「こんな形だと鋳造しても鋳型から取り出せないよ!」など、得られる形状に対してなんらかの条件を設けたいことが多々あります。 そういった種々の条件を考慮した最適形状を得るための機能が製造制約となります。
では、ノンパラメトリック形状最適化においてこれらのような制約はどのようにすれば実現できるのでしょうか。 OPTISHAPE-TSには数多くの製造制約が搭載されていますが、大きく分けると次の2つの方法に分類することができます。
1. \(H^1\) 勾配法におけるペナルティ項による制限
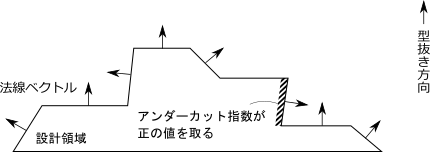
力法をイメージしていただくとわかりやすいのですが、感度に比例した外力を加えて形状の変動量を求める際に、製造制約を違反させないような剛性を付加する方法となります。 たとえば型抜き可能な形状にする制約の場合、あらかじめ決められた設計領域の表面について法線ベクトルが型抜き方向と直角な向きに近づくにつれて、その表面の回転移動に対する剛性をより大きくします。 感度で形を変えようとはするけど、制約を違反しそうな変形に対しては剛性が上がっているため形が変わりにくくなっているような感じですね。 このように、ペナルティの剛性を \(H^1\) 勾配法の処理のときに考慮することで結果的に製造制約を満たそうとするのがこの方法となります。

OPTISHAPE-TSでは形状変動制限と呼ばれる機能のほとんどがこの方法で実装されています。
2. 評価関数による制限
評価関数としてその製造制約の違反量を定量的に表し、それを制約関数として考慮することで制約の違反量をなくし、製造制約を満たそうとするのがこの方法になります。 たとえば、型抜き制約の場合は設計領域表面のアンダーカット部でなんらかの値を取り、そうでない領域で0になるようなアンダーカット指数というものを定義しておき、それを対象の表面で積分した評価関数を定義します。 この評価関数の感度がアンダーカット部の発生を抑えるようなものとなるので、他の制約関数と同じように考慮して最適化を行うことで型抜き制約を満たすことができるのです。
これら2つのアプローチはいずれも際立った計算時間やRAM容量を必要とせず、設定も容易(型抜き制約であれば対象とする領域と型抜き方向を指定するだけ)なので、使い勝手という観点では同等と言えます。 どちらの方法もすべての評価関数と自由に組み合わせて使うことができますし、異なる製造制約を複数設定することも可能です。
大きな違いとしては、次のものが挙げられます。 たとえば 1. の方法による制限は、制約を違反しそうな部分に剛性を付加して制約を違反しないようにするという原理なので、初期形状の段階で制約を違反しているような場合には用いることができません。 一方で 2. の方法であれば、制約を違反している部分に対してはその違反をなくすような感度が生じるので、初期形状で制約を違反していても問題はありません。
もともと、OPTISHAPE-TS の形状最適化には型抜きの制約を 1. の方法で実装した機能だけが搭載されていました。 しかしこのような問題点もあったため、バージョン2017で同じ製造制約を 2. の方法で実装した評価関数「アンダーカット」が追加されました[*1]。 先述したように、後者の機能であれば初期形状にアンダーカット部があっても型抜き制約を満たした最適形状を得ることができます。
*****
今回はOPTISHAPE-TSにおける製造制約の考え方についてご紹介しました。 同じ「型抜き制約」という条件を考慮するための機能として、形状変動制限の「型抜き」と評価関数の「アンダーカット」という2通りのものがあるのですが、その違いをご理解いただけたでしょうか。
≪脚注≫
[*1] 評価関数「アンダーカット」をご利用いただくには製造制約機能強化オプションが必要です。
★ご意見・ご感想はこちらへ★
![]() https://www.quint.co.jp/cgi-bin/qrepo-impr.cgi
https://www.quint.co.jp/cgi-bin/qrepo-impr.cgi
