第19話 ビード最適化
今回はOPTISHAPE-TSのノンパラメトリック最適化のひとつであるビード最適化についてご紹介します。
＊＊＊＊＊
ビードとは薄板状の構造に施される小さな凹凸形状のことです。 薄板の板厚を増やさずに構造物の特性を変えられるため、ビード生成の加工は色々なところで広く用いられている方法となります。 しかしビードの大きさや場所などはその特性を大きく左右するため、よりよいレイアウトを決めるのは時として非常に困難な場合があります。 そのレイアウトを構造最適化によって求める手法のひとつがビード最適化となります。
ビード形状は薄板を構成する物質点を法線方向に移動させることで生成することができます。 この移動量をビード高さと呼び、設計変数として最適化するのがビード最適化の考え方となります。 ビード高さは薄板上で分布する実数値関数として定義されるため、ビード最適化は形状最適化やトポロジー最適化と同じように関数の最適化（ノンパラメトリック最適化）として定式化することができます。
しかし凹凸のレイアウトを求めることを目的としているため、ビード高さには上限値 \(h\) を定めるのが一般的です。 そこで実際に最適化するのは 0 から 1 までの実数値を取るような関数 \(\phi\) にして、実際の高さはその関数に \(h\) をかけることで算出するようにします。
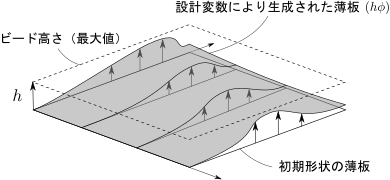
そう考えると、0 から 1 までの密度を表す関数を対象として最適化を行うトポロジー最適化との類似性も少し見えてきますね。 トポロジー最適化では中間密度と呼ばれる、材料が存在するかどうかがぼんやりとした領域が存在することが特徴のひとつでしたが、ビード最適化も同じように中間的な高さを含んだ結果が得られる場合があります。 製造上の都合で明瞭なレイアウトを得たい場合には好ましくない特徴ではありますが、たとえば中間的な高さに対してペナルティを与えるような評価関数を追加することで、ある程度は凹凸がはっきりとした結果を得ることができます（下図参照。コンターは設計変数を表す）。
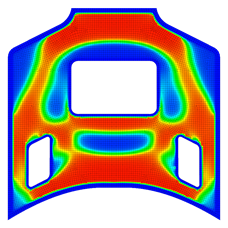
設計変数がこのように定義されれば、あとは定義された評価関数に対して感度（設計変数に対する評価関数の微分）を求めることで形状最適化やトポロジー最適化と同じ枠組みで最適化を行うことができます。 ただし、感度をそのまま使ってビード高さを更新すると形状最適化と同じような波打ち現象が生じてしまう場合があることがわかっています。 そこで \(H^1\) 勾配法を用いて感度を平滑化することにより、そのようなビード形状を回避するようにしています。
同じような最適化の手法としてトポグラフィ最適化と呼ばれるものがあります。 ビード形状を生成することを目的としている点は同じですが、こちらの方法ではビード形状をベーシスベクトルと呼ばれる単純な変形モードの線形結合で表現し、その重み係数を設計変数として最適化します。 つまり有限個の実数パラメータを対象とした最適化となるため、こちらの方法はパラメトリックな最適化に分類されます。 同じビード形状を対象とした最適化ではありますが、パラメトリックな方法であるトポグラフィ最適化とノンパラメトリックな方法であるビード最適化というふうに理解すれば、ノンパラメトリックな最適化の特徴を理解されている方であれば両者の違いは容易に解釈できるかと思います。
＊＊＊＊＊
今回はビード最適化についてご紹介しました。 弊社Webページではビード最適化の解析例もご紹介していますので、ご興味があればご覧いただければと思います。
★ご意見・ご感想はこちらへ★
https://www.quint.co.jp/cgi-bin/qrepo-impr.cgi
