第18話 関数の最大値を評価する:KS関数
OPTISHAPE-TS では「最大Mises応力」や「最大変位」など、そのモデル上で分布する関数の最大値を評価することができます。 しかし文字通り最大値をそのまま評価関数とすると微分を評価することができなくなるため、感度を求められなくなってしまいます。 今回は、OPTISHAPE-TSで採用しているKS関数と呼ばれるものを用いた最大値の評価方法についてご紹介します。
*****
KS関数のKSは、この関数の発案者であるG. KreisselmeierとR. Steinhauserの頭文字から来ています。 その基本的な考え方は、指数関数 \(\exp(x) = \mathrm{e}^x\) (\(\mathrm{e}\) は自然対数の底)の爆発的な増加性、つまり少し \(x\) を大きくしただけで関数の値が非常に大きくなるという性質を利用したものとなります。
はじめに簡単な例として、次の数列の最大値を求める問題を考えてみましょう: \[ \{a_n\} = \{3.1, 4.1, 5.9, 2.6, 5.3\}. \]
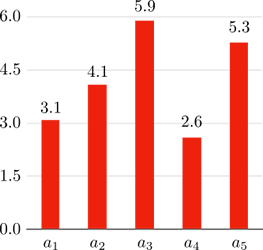
もちろん \(\{a_n\}\) の最大値は 5.9 です。 ここではこの値を近似する関数を考えることになります。 そのために、数列を入力として実数値を返す次のような関数 \(\kappa_{\mathrm{D}} : \mathbb{R}^n \to \mathbb{R}\) を考えます: \[ \kappa_{\mathrm{D}}(\{a_n\}) = \ln \left(\sum_{i = 1}^{n} \exp(a_i)\right). \] 対数関数 \(\ln\) は指数関数 \(\exp\) の逆関数なので、ある値にこれら2つの関数を順に作用させるともとの値に戻ります。 一方で、数列の各項に対して指数関数を作用させると、上述した爆発的な増加性によって最大値に対する差が大きく強調されます。
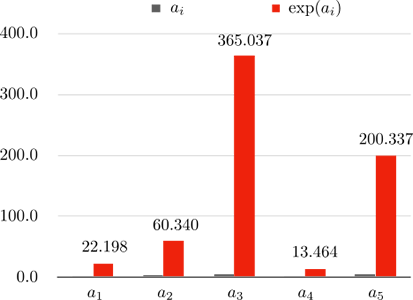
このとき、それらの総和 \(\sum_i \exp(a_i)\) は各項の最大値 \(\max_i\{\exp(a_i)\}\) に近い値を取るようになります。 それを対数関数でもとの値に戻すことになるため、この関数によって数列の最大値を近似することができるのです。
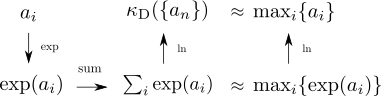
実際にこの関数に数列 \(\{a_n\}\) を代入して計算してみると、 \[ \kappa_{\mathrm{D}}(\{a_n\}) = 6.49432 \] のようになります。
ただし、指数関数を爆発的に増加させるためには入力とする値をある程度大きくする必要があります。
言い換えれば、数列の各項があまり大きくないと近似される値の精度が悪くなってしまいます。
実際、先ほど求めた近似値にも1割ほどの相対誤差が生じています。
そこで、各項を定数倍してある程度大きくしてからKS関数を使って近似し、最後にその定数で割ってもとに戻すという手順を追加します。
具体的には、正の実定数 \(\rho\) をあらかじめ定めておいて
\[
\kappa_{\mathrm{D}}(\{a_n\}) = \dfrac{1}{\rho} \ln \left(\sum_{i = 1}^{n} \exp(\rho a_i)\right)
\]
のように \(\kappa_{\mathrm{D}}\) を定義し直します。
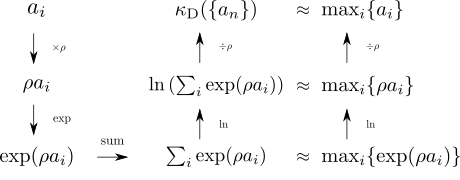
以上の考え方を離散的な考え方(\(\sum\))から連続的な考え方(\(\int\))に応用したときのKS関数は \[ \kappa_{\mathrm{C}}(f) = \dfrac{1}{\rho} \ln \left(\int_{\Omega} \exp(\rho f) \,\mathrm{d}x \right) \] のように定義されます。 \(f\) は \(\Omega\) 上で分布する実数値関数で、最大値を近似したい関数となります。 つまり、\(\kappa_{\mathrm{C}}\) は \(\Omega\) 上で定義された関数 \(f\) を受け取って実数値(最大値の近似値)を返すような関数(汎関数)ということになります。 最大値を近似する論理は先ほどの数列の場合と同じで、指数関数で最大値を際立たせてから対数関数でもとに戻すというものになります。
これをMises応力の評価に適用すると、\(\Omega\) は解析対象とするモデル、\(f\) はMises応力を表す関数、 そして\(\kappa_{\mathrm{C}}\) は \(f\) の最大値を近似するため最大Mises応力を表すこととなります。 重要なのは、KS関数が通常の最大値を表す \(\max\) とは異なって微分を評価できるという点です。 KS関数の値を評価することで、間接的にMises応力の最大値を評価しているのです。
*****
今回はモデル上での最大値を評価するために使われるKS関数の考え方について解説しました。 OPTISHAPE-TSをお使いの方はマニュアルなどで名前だけは目にされたことがあったという方もいらっしゃるかと思いますが、その中身はこのようなものだったということがおわかりいただけたのであれば幸いです。 もととなっている論文は以下に示しましたので、もしご興味があればご覧いただければと思います。
- G. Kreisselmeier and R. Steinhauser, Systematic Control Design by Optimizing a Vector Performance Index, IFAC Proceedings Volumes, Volume 12, Issue 7, 1979, pp. 113-117.
- 下田昌利, 畔上秀幸, 桜井俊明, 形状最適化におけるミニマックス問題の数値解法(最大応力と最大変位の最小設計), 日本機械学会論文集 A編, 63 (607), 1997, pp. 610-617.
★ご意見・ご感想はこちらへ★
![]() https://www.quint.co.jp/cgi-bin/qrepo-impr.cgi
https://www.quint.co.jp/cgi-bin/qrepo-impr.cgi
