第21話 コンプライアンスってなに?
OPTISHAPE-TSのノンパラメトリック最適化(形状最適化、トポロジー最適化、ビード最適化)では、線形弾性解析におけるコンプライアンスを共通して評価することができます。 いつもお使いいただいている方からすれば「あぁ、コンプライアンスね」と他愛もない話かと思いますが、そうでない方からときおり「コンプライアンスってなに?」というご質問をいただくことがあります。 今回の記事では、このコンプライアンスについて少し丁寧に解説してみようと思います。
*****
コンプライアンスという言葉はビジネスの場面で耳にすることのほうがより一般的ですが、こちらでは「決まりを遵守すること」という意味があります。 「あらかじめ与えられたものに従うこと」という意味から転じて、機械系の分野では「外力に対する変形のしやすさ」という意味を持ち、剛性(=「外力に対する変形のしにくさ」)の逆数のような指標として使われています。
変形のしやすさと言われても非常に漠然としていますね。 具体的には外力仕事、つまり荷重とそれが与えられた部分の変位の積を足し合わせた値として定義されます。 例として、下図のような長さ \(l\)、断面積 1 の1次元片持ち梁に物体力 \(b\) と境界力 \(p\) を与える問題を考えてみましょう。
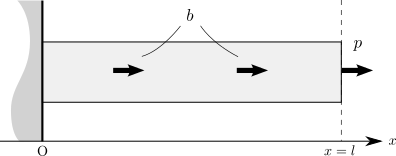
図に示した梁の微小変形をモデル化する偏微分方程式の境界値問題(線形弾性問題)は、変位を \(u\) とすると \[ \begin{align} -\dfrac{\mathrm{d} \sigma}{\mathrm{d}x} &= b, \\ u(0) &= 0, \\ \sigma(l) &= p \end{align} \] のように与えられます。 ただし、\(E\) を梁のYoung率として、応力とひずみをそれぞれ \[ \begin{align} & \sigma(u) = E\varepsilon(u), \\ & \varepsilon(u) = \dfrac{\mathrm{d}u}{\mathrm{d}x} \end{align} \] とおきました。 これらを代入すれば、線形弾性問題は \[ \begin{align} -E\dfrac{\mathrm{d^2} u}{\mathrm{d}x^2} &= b, \\ u(0) &= 0, \\ E\dfrac{\mathrm{d}u}{\mathrm{d}x}(l) &= p \end{align} \] のように書き換えることもできますね。
このとき、外力仕事は物体力がする仕事 \[ \int_{0}^{l} b \cdot u \,\mathrm{d}x \] と境界力がする仕事 \[ p \cdot u(l) \] の和となります。 それがそのままコンプライアンスの定義とされるので、評価関数の定義としては \[ f(u) = \int_{0}^{l} b \cdot u \,\mathrm{d}x + p \cdot u(l) \] のようになります。 線形弾性問題を解いて変位 \(u\) が得られると、そのときのコンプライアンス \(f\) の値を計算できるという流れになるわけですね。 今回は1次元の場合で説明しましたが、2次元でも3次元でも考え方は同じです。
*****
さて、コンプライアンスと同じ文脈で平均コンプライアンスという言葉が使われるのをご存知の方もいらっしゃるかと思いますが、この「平均」って一体なんなのでしょうか。 これには、強制変位によって弾性体を変形させたときの剛性の評価方法が関わってきます。
先ほどの梁の支配方程式で物体力を \(b = 0\) にし、右端に境界力 \(p\) を与える代わりに強制変位 \(u_{\mathrm{D}}\) を与える問題 \[ \begin{align} -\dfrac{\mathrm{d}\sigma}{\mathrm{d}x} &= 0, \\ u(0) &= 0, \\ u(l) &= u_{\mathrm{D}} \end{align} \] を考えてみましょう。 この問題では外力を陽に作用させていないため、剛性の指標として外力仕事を用いることができません。 ではこのときの剛性はどのようにすれば評価できるのでしょうか。
強制変位を作用させた部分には反力、すなわち与えた強制変位を元に戻そうとする抵抗力が生じます。 この力は梁の右端における応力とつり合うので、 \[ -\sigma(l) \] として求められます。 言い換えると、強制変位 \(u_{\mathrm{D}}\) を生じさせるためにこの負値に相当する力を作用させていることになるので、強制変位 \(u_{\mathrm{D}}\) がした仕事は \[ \sigma(l) \cdot u_{\mathrm{D}} \] に相当するものとなります。 剛性というものを考えたときに、この仕事がより大きい方が変形に対してより強く抵抗していることになるので、このときのコンプライアンス(変形のしやすさ)の定義としては負号をつけて \[ f(u) = -\sigma(l) \cdot u_{\mathrm{D}} \] のようにするのがよさそうです。 \(f\) の値が小さいということは強制変位がした仕事が大きい、すなわち変形に抵抗する力が大きいということになるため、剛性が大きいということに繋がります。
そこで最初のコンプライアンスの定義に先述した項を追加して \[ f(u) = \int_{0}^{l} b \cdot u \,\mathrm{d}x + p \cdot u(l) - \sigma(l) \cdot u_{\mathrm{D}} \] のように拡張したものが平均コンプライアンスと呼ばれます。 コンプライアンスは外力仕事と同義であるものとして定義されていましたが、第3項は外力仕事と呼べるものではないため、平均的な外力仕事(コンプライアンス)という意味合いからこのように名付けられたのです。 つまり強制変位が作用していない問題であれば、コンプライアンスと平均コンプライアンスはまったく同じものを指すことになりますね。
*****
今回は線形弾性解析におけるコンプライアンスについて解説しました。 外力仕事としての定式化と平均コンプライアンスの定義について理解を深めていただけたでしょうか。
★ご意見・ご感想はこちらへ★
![]() https://www.quint.co.jp/cgi-bin/qrepo-impr.cgi
https://www.quint.co.jp/cgi-bin/qrepo-impr.cgi
