第22話 コンプライアンスの感度 その1「2次元の設計変数による問題」
前回の記事では線形弾性問題におけるコンプライアンスについて解説しました。 ところで、「コンプライアンスの感度はひずみエネルギーである」ということを耳にされたことがある方もいらっしゃるかと思いますが、これはどのようにして導出されるのでしょうか。 そこで今回から数回に渡って、コンプライアンスの感度の導出について見てみたいと思います。 ここでも、前回の記事で用いた片持ち梁の線形弾性問題を例として考えることにします。
*****
まずはじめに、最適化問題を考えるにあたって最も重要なもののひとつである設計変数を導入しましょう。 ここでは簡単な例として、片持ち梁の断面積を左半分では \(\require{physics} a_1\)、右半分では \(a_2\) として、これら2つの値を設計変数とします。 このときコンプライアンスの感度とは、それぞれの断面積を微小に変化させたときにコンプライアンスの値がどれぐらい変化するかを表す値となります。 このような梁に対して、前回と同じように物体力 \(b\) と境界力 \(p\) を作用させます。 ただし、今回は境界力 \(p\) を作用部分の面積 \(a_2\) に依存しない点荷重として扱うことにします。
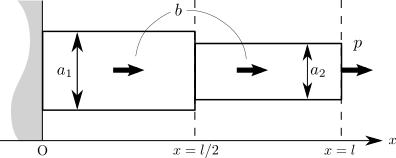
これからしようとしていることは次のようになります。 まずはじめに、断面積が \(a_1\)、\(a_2\) となった1次元片持ち梁について前回の記事と同じようにして変形を支配する方程式を導きます。 次に、そうして構成した線形弾性問題の解である変位を使ってコンプライアンスを定義します。 最後にコンプライアンスを断面積で微分して、その感度を求めます。 少々数式が多くなりますが、なるべく要点だけを抑えながら解説していこうと思います。
*****
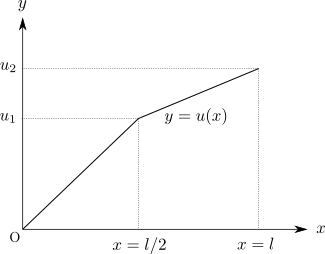
では、このように定義された断面積を持つ1次元片持ち梁の変形を定める問題を見ておきましょう。 ここでは \(x = l/2\) と \(x = l\) における変位をそれぞれ \(u_1\) および \(u_2\) として、梁内部における変位はこれらの線形補間によって \[ u(x) = \begin{cases} \dfrac{2u_1}{l}x & \qty(0 \leq x \leq \dfrac{l}{2}) \\ \dfrac{2\qty(u_2 - u_1)}{l}x + 2u_1 - u_2 & \qty(\dfrac{l}{2} \leq x \leq l) \end{cases} \] のように得られるものと仮定します。 これは、左右2つの梁がそれぞれ両端だけに節点を持つような、いわゆる1次要素によって変形がモデル化されていることになります。 つまり、関数 \(u\) を求めるかわりに、上記の補間式における節点値 \(u_1\)、\(u_2\) を求めることになります。
続いて、このような梁における変位の節点値 \(u_1\)、\(u_2\) を定めるような支配方程式を示しておきます。 導出については長くなるので割愛しますが、前回の記事で示した線形弾性問題の式に断面積を考慮したものと上記の変位 \(u\) の式を使えば、変位の節点値 \(u_1\)、\(u_2\) が満たすべき式は次のような連立1次方程式 \[ \dfrac{2E}{l}\mqty(a_1 + a_2 & -a_2 \\ -a_2 & a_2) \mqty(u_1 \\ u_2) = \dfrac{1}{4}bl\mqty(a_1 + a_2 \\ a_2 ) + p\mqty(0 \\ 1) \] になります。 ここで、前回の記事と同様に \(E\) は Young 率を表す定数としています。
この式を見ると、俗に言う剛性行列と外力ベクトルがそれぞれ \[ \begin{align} & \bar{\vb*{K}} = \dfrac{2E}{l}\mqty(a_1 + a_2 & -a_2 \\ -a_2 & a_2), \\ & \bar{\vb*{f}} = \dfrac{1}{4}bl\mqty(a_1 + a_2 \\ a_2 ) + p\mqty(0 \\ 1) \end{align} \] となっており、両者とも設計変数 \(a_1\)、\(a_2\) の関数となっていることがわかります。 設計変数の値が決まることで剛性行列や外力ベクトルの値が決まり、解くべき方程式が定まって変位 \(u_1\)、\(u_2\) を求めることができるようになります。 そういう意味で、この問題において変位 \(u_1\)、\(u_2\) は設計変数 \(a_1\)、\(a_2\) の関数になっているとも言えるわけです。
*****
続いて、今回の問題におけるコンプライアンスの評価関数を確認しておきましょう。 前回の記事でお話ししたコンプライアンスは、物体力がする仕事と境界力がする仕事の和として \[ f\qty(u) = \int_0^l bu \dd{x} + pu\qty(l) \] のように定義していました。 第2項についてはそのままでOKですが、第1項の物体力がする仕事については体積の積分にあたって断面積 \(a\) を考慮しなければならないため、 \[ \int_0^l b u \dd{x} \to \int_0^l a b u \dd{x} \qty(= \int_0^{l/2} a_1 b u \dd{x} + \int_{l/2}^l a_2 b u \dd{x}) \] のように直す必要があります。
こうして書き直したコンプライアンスの定義に上述した変位 \(u\) の式を代入して整理すれば、今回の問題におけるコンプライアンスは \[ f\qty(a_1, a_2, u_1, u_2) = \dfrac{1}{4}bl \qty{\qty(a_1 + a_2)u_1 + a_2 u_2} + pu_2 \] となります。 コンプライアンスが断面積 \(a_1\)、\(a_2\) と変位 \(u_1\)、\(u_2\) の関数として定義されるという点を抑えていただければと思います。
*****
さて、ようやく2つの断面積を設計変数にしたときのコンプライアンスを定義できたところまで来たのですが、長くなったので続きは次回となります。 感度はコンプライアンスを設計変数で微分することで得られるのですが、そのコンプライアンスには設計変数だけでなく変位の節点値 \(u_1\)、\(u_2\) も含まれており、この変位も設計変数の関数になっているのでした。 このような場合に、どのようにして設計変数に対する微分を求めるのかを次回の記事で見ていきます。
参考文献
- 畔上秀幸, 形状最適化問題, 森北出版(1.1 節, 6.1 節)
★ご意見・ご感想はこちらへ★
![]() https://www.quint.co.jp/cgi-bin/qrepo-impr.cgi
https://www.quint.co.jp/cgi-bin/qrepo-impr.cgi
