第23話 コンプライアンスの感度 その2「代入法と直接微分法」
前回の記事から、コンプライアンスの感度を導出してみようという話が始まりました。 この記事はその第2回で、設計変数に対するコンプライアンスの微分を考えてみます。
*****
前回の記事の要点を簡単にまとめておきます。 2つの断面積 \(a_1\)、\(a_2\) を持つ片持ち梁があり、変位が節点値 \(u_1\)、\(u_2\) の線形補間で得られると仮定すると、それらが満たすべき方程式(状態方程式)は \[ \require{physics} \bar{\vb*{K}} \bar{\vb*{u}} = \bar{\vb*{f}}, \quad \bar{\vb*{u}} = \mqty(u_1 \\ u_2) \] という連立1次方程式となるのでした。 ここで、剛性行列 \(\bar{\vb*{K}}\) と外力ベクトル \(\bar{\vb*{f}}\) はそれぞれ \[ \begin{align} \bar{\vb*{K}} = \dfrac{2E}{l} \mqty(a_1 + a_2 & -a_2 \\ -a_2 & a_2), \quad \bar{\vb*{f}} = \dfrac{1}{4}bl \mqty(a_1 + a_2 \\ a_2) + p \mqty(0 \\ 1) \end{align} \] となりました。 そして、この問題におけるコンプライアンスは \[ f\qty(a_1, a_2, u_1, u_2) = \dfrac{1}{4}bl \qty{\qty(a_1 + a_2)u_1 + a_2 u_2} + pu_2 \tag{1} \] のように定義されるのでした。
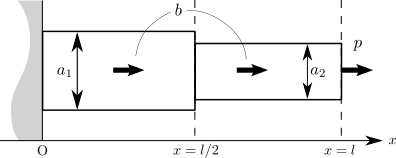
今回はコンプライアンス \(f\) の設計変数 \(a_1\)、\(a_2\) に対する微分を求めてみましょう。 しかし前回の記事の最後でも少し触れたように、変位 \(u_1\)、\(u_2\) は本来設計変数 \(a_1\)、\(a_2\) の関数となっており、言うなれば \(f\qty(a_1, a_2, u_1\qty(a_1, a_2), u_2\qty(a_1, a_2))\) のようになっています。 このような形となっている \(f\) の設計変数 \(a_1\)、\(a_2\) に対する微分について、その求め方を考えてみましょう。
*****
はじめに考えられる方法としては、状態方程式を使ってコンプライアンス \(f\) から変位 \(u_1\)、\(u_2\) を消去するものがあります。
設計変数 \(a_1\) と \(a_2\) がともに0ではないとき、剛性行列 \(\bar{\vb*{K}}\) には逆行列 \[ \bar{\vb*{K}}^{-1} = \dfrac{l}{2Ea_1 a_2} \mqty(a_2 & a_2 \\ a_2 & a_1 + a_2) \] が存在するので、 \[ \bar{\vb*{u}} = \bar{\vb*{K}}^{-1} \bar{\vb*{f}} = \dfrac{bl^2}{8E} \mqty(1 + 2 a_2 / a_1 \\ 2 + 2 a_2 / a_1) + \dfrac{pl}{2E} \mqty(1 / a_1 \\ 1 / a_1 + 1 / a_2) \tag{2} \] のように変位 \(u_1\)、\(u_2\) を設計変数 \(a_1\)、\(a_2\) で表すことができるようになります。 これをコンプライアンス \(f\) の式 \((1)\) に代入すれば変位 \(u_1\)、\(u_2\) を消去することができ、\(f\) は設計変数 \(a_1\)、\(a_2\) だけの関数となるので、設計変数に対する微分を単純に求められるようになります。 結果として得られるのは \(a_1\) と \(a_2\) で表される長い式となるだけなので、ここでは具体的に書き下すことは省略します。 このようにして微分を求める方法は代入法と呼ばれます。
*****
次に考えられる方法としては、合成関数に対する微分の連鎖律を用いるものがあります。 少々長くなりますが、具体的に数式を追ってみようと思います。
今回の場合は、たとえば \(a_1\) に対する \(f\) の微分は \[ \dv{f}{a_1} = \pdv{f}{a_1} + \pdv{f}{u_1}\pdv{u_1}{a_1} + \pdv{f}{u_2}\pdv{u_2}{a_1} \] のように複数の偏微分の積で表すことができます。 以下では右辺の5つの偏微分のそれぞれを求めてみましょう。
まず、最初の \[ \pdv{f}{a_1} = \dfrac{1}{4}bl u_1 \] の項は \(f\) の定義の式 \((1)\) から簡単に計算できます。 続いて、\(\pdv*{f}{u_1}\) と \(\pdv*{f}{u_2}\) は同様に \(f\) の定義からも求められるのですが、ここでは \(f = \bar{\vb*{f}}\cdot\bar{\vb*{u}}\) が成り立つことから(\(f\) がコンプライアンスを、\(\bar{\vb*{f}}\) が外力ベクトルを表すことにご注意ください)、 \[ \mqty(\pdv{f}{u_1} \\ \pdv{f}{u_2}) = \bar{\vb*{f}} \] のようになることを利用します。 残りの2つの \(\pdv*{u_1}{a_1}\) と \(\pdv*{u_2}{a_1}\) は先ほど陽に求めた \(\bar{\vb*{u}}\) を \(a_1\) で偏微分しても求められるのですが、状態方程式の両辺を \(a_1\) で偏微分した式から求めることもできます。 具体的には次のようにします。 まず、状態方程式 \(\bar{\vb*{K}} \bar{\vb*{u}} = \bar{\vb*{f}}\) の左辺の偏微分 \[ \pdv{a_1} \qty(\bar{\vb*{K}} \bar{\vb*{u}}) = \pdv{\bar{\vb*{K}}}{a_1} \bar{\vb*{u}} + \bar{\vb*{K}} \pdv{\bar{\vb*{u}}}{a_1} \] と右辺の偏微分 \[ \pdv{\bar{\vb*{f}}}{a_1} \] が一致するという式を変形することで、 \[ \begin{align} \pdv{\bar{\vb*{K}}}{a_1} \bar{\vb*{u}} + \bar{\vb*{K}} \pdv{\bar{\vb*{u}}}{a_1} & = \pdv{\bar{\vb*{f}}}{a_1} \\ \pdv{\bar{\vb*{u}}}{a_1} & = \bar{\vb*{K}}^{-1}\qty(-\pdv{\bar{\vb*{K}}}{a_1} \bar{\vb*{u}} + \pdv{\bar{\vb*{f}}}{a_1}) \end{align} \] という式を得ることができます。 \(\bar{\vb*{K}}^{-1}\) についてははじめの方法の中で求めたとおりで、\(\bar{\vb*{K}}\) と \(\bar{\vb*{f}}\) の \(a_1\) に対する偏微分についてはこれらの定義から \[ \pdv{\bar{\vb*{K}}}{a_1} = \dfrac{2E}{l} \mqty(1 & 0 \\ 0 & 0), \quad \pdv{\bar{\vb*{f}}}{a_1} = \dfrac{1}{4}bl \mqty(1 \\ 0) \] のように簡単に計算できます。
以上で求めた偏微分を使えば、\(f\) の微分は \[ \begin{align} \dv{f}{a_1} & = \pdv{f}{a_1} + \pdv{f}{u_1}\pdv{u_1}{a_1} + \pdv{f}{u_2}\pdv{u_2}{a_1} = \pdv{f}{a_1} + \pdv{f}{\vb*{u}}\cdot\pdv{\bar{\vb*{u}}}{a_1} \\ & = \dfrac{1}{4}bl u_1 + \bar{\vb*{f}} \cdot \qty(\bar{\vb*{K}}^{-1}\qty(-\pdv{\bar{\vb*{K}}}{a_1}\bar{\vb*{u}} + \pdv{\bar{\vb*{f}}}{a_1})) \\ & = \dfrac{1}{4}bl u_1 + \bar{\vb*{u}} \cdot \qty(-\pdv{\bar{\vb*{K}}}{a_1}\bar{\vb*{u}} + \pdv{\bar{\vb*{f}}}{a_1}) \\ & = \dfrac{1}{4}bl u_1 - \dfrac{2E}{l}u_1^2 + \dfrac{1}{4}bl u_1 \\ & = \dfrac{1}{2}bl u_1 - \dfrac{2E}{l}u_1^2 \end{align} \] のような \(u_1\) を使った式にまとめられます。 ここで、2行目から3行目への式変形で状態方程式を変形した式 \((2)\) を用いました。 この式は、断面積 \(a_1\) の部分における応力 \(\sigma_1 = E \varepsilon_1\) とひずみ \(\varepsilon_1 = 2u_1/l\) を用いることで、 \[ \dv{f}{a_1} = \dfrac{l}{2} \qty(bu_1 - \sigma_1\varepsilon_1) \] のように表すことができます。
ここで出てきた \(l\sigma_1\varepsilon_1/2\) は断面積 \(a_1\) の部分におけるひずみエネルギー密度を表します。 式変形が長くなりましたが、評価関数の設計変数に対する微分を求めると、結果としてひずみエネルギー密度が現れることがとりあえず確認できたことになります。 このように微分の連鎖律を用いた方法は直接微分法と呼ばれます。 もちろん、この結果は代入法の結果と一致します。 \(\bar{\vb*{u}}\) を \(a_1\)、\(a_2\) で表した式 \((2)\) を代入すれば確かめられるはずです。
以上の流れを \(a_2\) にしても同じように適用することで、\(a_2\) に対する \(f\) の微分も求めることができます。 結果だけ示しておくと、断面積 \(a_2\) の部分における応力 \(\sigma_2 = E\varepsilon_2\) とひずみ \(\varepsilon_2 = 2\qty(u_2 - u_1)/l\) を用いて \[ \dv{f}{a_2} = \dfrac{l}{2}\qty(b\qty(u_1 + u_2) - \sigma_2 \varepsilon_2) \] となります。
*****
3つ目の方法として Lagrange 乗数法と呼ばれる手法を用いるものがありますが、長くなりますので続きはまた次回とします。 今回は
- 代入法:
評価関数から状態変数を消去して、設計変数に対するコンプライアンスの微分を求める方法 - 直接微分法:
微分の連鎖律を用いて、設計変数に対するコンプライアンスの微分を求める方法
の2つを紹介しました。
★ご意見・ご感想はこちらへ★
![]() https://www.quint.co.jp/cgi-bin/qrepo-impr.cgi
https://www.quint.co.jp/cgi-bin/qrepo-impr.cgi
