第24話 Lagrange 乗数法
前回の記事から、コンプライアンスの感度を導出してみようという話が始まりました。 今回はその第3回で、Lagrange 乗数法について解説します・・・と思ったのですが、話が長くなるので今回は感度の導出という意味では一旦休憩を挟んで、Lagrange 乗数法そのものの解説をしたいと思います。
*****
大学の解析学の授業などで学んだことがあるという方もいらっしゃるかと思いますが、Lagrange 乗数法(あるいは Lagrange の未定乗数法)を一言で説明すると、等式で表される制約条件のもとである関数の値が極値となるときに、その変数が満たすべき条件を表すための方法となります。 この方法を応用することでコンプライアンスの感度を導出することができるのですが、それに先立って今回は簡単な例題を通して Lagrange 乗数法が意味するところのイメージをつかんでもらいたいと思います。
ここでは等式制約付きの最適化問題の簡単な例題として、「面積が一定のもとで周の長さが最小になるような長方形の2辺の長さを求める問題」を考えてみましょう。 なんとなくわかるかもしれませんが、答えは2辺の長さが同じ長方形、つまり正方形となります。 ここでは求めるべき長方形の縦の長さを \(\require{physics} x_1\)、横の長さを \(x_2\) として、それらをまとめて \(\vb*{x} = \qty(x_1, x_2)\) と書くことにします。
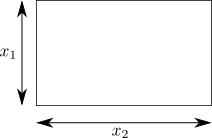
ここで、周の長さを表す目的関数は \[ f_0\qty(\vb*{x}) = 2x_1 + 2x_2 \] として定義します。 また、面積を表す制約関数を \[ f_1\qty(\vb*{x}) = x_1 x_2 - c \] として定義します。 ここで、\(c\) はあらかじめ決められた面積を表す正の定数とします。 これらの評価関数を使って、解くべき問題は「\(f_1\qty(\vb*{x}) = 0\) を満たした上で \(f_0\qty(\vb*{x})\) を最小にするような \(\vb*{x}\) を求める問題」として定式化されます。
ちなみに、今回の目的関数 \(f_0\) と制約関数 \(f_1\) のグラフの概形はそれぞれ下の図のようになります。
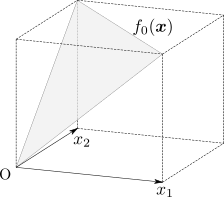
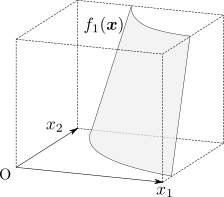
さて、このように最適化問題が定式化されたとき、最適解はどのような条件を満たしていることになるでしょうか。 まず考えられるのは、最適解は \(f_1\qty(\vb*{x}) = 0\) を満たしていなければならないということです。 これを言い換えると、最適解は制約関数 \(f_1\) のグラフと \(x_1 x_2\) 平面が交わる曲線(双曲線)上の点である必要があるということになります。 ここではこの曲線を \(C\) とします。
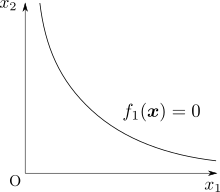
他にはどのような条件を満たす必要があるでしょうか。 ここで制約がない問題のときのことを考えてみると、たとえば目的関数の勾配がゼロベクトルであることが考えられました。 そこで、とりあえず目的関数の勾配を求めてみましょう。 目的関数の勾配は、目的関数を \(x_1\) と \(x_2\) のそれぞれで偏微分することで \[ \grad f_0\qty(\vb*{x}) = \mqty(\pdv{f_0}{x_1} \\ \pdv{f_0}{x_2}) = \mqty(2 \\ 2) \] のように計算できます。 つまり、目的関数の勾配 \(\grad f_0\) は \(x_1\) と \(x_2\) の値に関係なく、常に一定の方向を向いているということになります。 これだけでは勾配がゼロベクトルになるような \(\vb*{x}\) は存在しないことになり、制約がない問題のときと同じ条件を当てはめて考えることはできなさそうだということがわかります。
次に制約関数の勾配でも求めてみましょうか。 こちらは \[ \grad f_1\qty(\vb*{x}) = \mqty(\pdv{f_1}{x_1} \\ \pdv{f_1}{x_2}) = \mqty(x_2 \\ x_1) \] となります。 曲線 \(C\) 上における勾配 \(\grad f_1\) は次の図のように、曲線 \(C\) の接線に直交するような向きとなることがわかります。
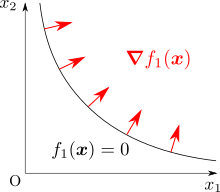
ここで、\(\grad f_1\) に重ねて \(-\grad f_0 \qty(\vb*{x}) = \qty(-2, -2)\) を描いてみましょう。
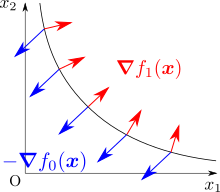
\(\grad f_0\) は \(f_0\) が最も増加する方向なので、\(-\grad f_0\) は \(f_0\) が最も減少する方向を表します。 \(-\grad f_0\) と \(\grad f_1\) が真逆の向きになっていないところ(図中の中央以外の部分)では、まだ \(-\grad f_0\) の方向に進んで \(f_0\) を減少させる余地が残っている、というふうに見ることができるかと思います。 逆に、\(-\grad f_0\) と \(\grad f_1\) が真逆の向きになっているところ(図中の中央の部分)では、曲線 \(C\) 上の点の中では最も \(f_0\) が小さくなっているということが言えます。 首を右に45度傾けて眺めてみると、まるで曲線 \(C\) 上を転がる質点に青い矢印の一様な下向きの重力と、赤い矢印の垂直抗力(厳密に言うと大きさは違いますが)が働いていて、両者が真逆の向きになる中央へと質点を運ぼうとしているような様子がイメージできるでしょうか。
このように、\(\vb*{x}\) が最適解であればその点における目的関数の勾配 \(\grad f_0\) と制約関数の勾配 \(\grad f_1\) が真逆の向きとなることがわかります。
ただ、よくよく考えてみると制約関数の定義は
\[
f_1\qty(\vb*{x}) = c - x_1 x_2
\]
のように中身の符号をひっくり返して問題を考えてもよいことがわかります。
この場合は上の図の赤い矢印の向きも180度変わることになり、最適解における \(\grad f_0\) と \(\grad f_1\) の向きはまったく同じとなります。
まとめると、\(\vb*{x}\) が最適解であれば \(\grad f_0\) と \(\grad f_1\) が同じあるいは真逆の向きとなる、すなわち
\[
\grad f_0\qty(\vb*{x}) + \lambda \grad f_1\qty(\vb*{x}) = \vb*{0}
\]
となるような実数
今回の問題の場合は、この方程式は \[ \mqty(2 \\ 2) + \lambda \mqty(x_2 \\ x_1) = \mqty(0 \\ 0) \] となります。 この式と \(f_1\qty(\vb*{x}) = 0\) とを連立させることで、最適解である \[ \mqty(x_1 \\ x_2 \\ \lambda) = \mqty(\sqrt{c} \\ \sqrt{c} \\ -\dfrac{2}{\sqrt{c}}) \] が得られます。
*****
これまでの話をまとめると、\(\vb*{x}\) がこの問題における最適解ならば、\(\vb*{x}\) は次の2つの条件を満たすことになります。
- \(\grad f_0\qty(\vb*{x}) + \lambda \grad f_1\qty(\vb*{x}) = \vb*{0}\) を満たす \(\lambda\) が存在する。
- \(f_1\qty(\vb*{x}) = 0\) が成り立つ。
これらの条件を1つにまとめるために使われるのが Lagrange 関数と呼ばれる関数で、今回の問題の場合は \[ \mathscr{L}\qty(\vb*{x}, \lambda) = f_0\qty(\vb*{x}) + \lambda f_1\qty(\vb*{x}) \] のように定義されます。 \(\mathscr{L}\) はローマ字 L の花文字と呼ばれるもので、なにか特別な意味合いのある変数や関数であるということを強調するためにこのような変わった書体を使うことがあります。 Lagrange 関数 \(\mathscr{L}\) の \(\vb*{x}\) に対する停留条件、すなわち \(\vb*{x}\) で偏微分することで得られる \[ \pdv{\mathscr{L}}{\vb*{x}}\qty(\vb*{x}, \lambda) = \grad f_0\qty(\vb*{x}) + \lambda \grad f_1\qty(\vb*{x}) \] がゼロベクトルになるという条件が上記の 1. と同じものとなり、\(\lambda\) に対する停留条件、すなわち \(\lambda\) で偏微分することで得られる \[ \pdv{\mathscr{L}}{\lambda}\qty(\vb*{x}, \lambda) = f_1\qty(\vb*{x}) \] がゼロになるという条件が上記の 2. と同じものとなります。 互いに関係のなかった2つの条件が Lagrange 関数 \(\mathscr{L}\) の停留条件という(見かけは)1つの条件に置き換えられたことになりますね。
ここで使われた変数 \(\lambda\) は Lagrange 乗数と呼ばれます。 Lagrange 乗数を導入して Lagrange 関数を定義し、その停留条件を使って等式制約付きの最適化問題の解が満たすべき必要条件を表すのが Lagrange 乗数法ということになります。 制約関数が複数ある場合でも、同じ数だけ Lagrange 乗数を用意することによって、同じ考え方で満たすべき条件を記述することができます。
*****
今回は Lagrange 乗数法を使った感度の導出に先立って、一般的な Lagrange 乗数法の考え方を簡単な問題を通して解説しました。 要点をかいつまんで話を進めたので本当はもう少し議論しないといけない点もあるのですが、Lagrange 関数と Lagrange 乗数の2つを使った考え方の概要をつかんでいただけたのであれば幸いです。
★ご意見・ご感想はこちらへ★
![]() https://www.quint.co.jp/cgi-bin/qrepo-impr.cgi
https://www.quint.co.jp/cgi-bin/qrepo-impr.cgi
