第25話 コンプライアンスの感度 その3「Lagrange 乗数法」
前回の記事では等式制約付きの最適化問題における解が満たすべき条件としての Lagrange 乗数法を紹介しました。 今回はその考え方を応用して、コンプライアンスの感度を導出することを考えます。
*****
はじめに、今回の問題をもう一度おさらいしておきましょう。 断面積 \(\require{physics} \bar{\vb*{a}} = (a_1, a_2)^\mathsf{T}\) の1次元片持ち梁に外力を与えたときの変形 \(\bar{\vb*{u}} = \qty(u_1, u_2)^\mathsf{T}\) を支配する方程式が、剛性行列 \(\bar{\vb*{K}}\qty(\bar{\vb*{a}})\) と外力ベクトル \(\bar{\vb*{f}}\qty(\bar{\vb*{a}})\) を用いて \[ \bar{\vb*{K}}\qty(\bar{\vb*{a}})\bar{\vb*{u}} = \bar{\vb*{f}}\qty(\bar{\vb*{a}}) \tag{1} \] という連立1次方程式で得られていました。 このとき、コンプライアンスを表す評価関数は \[ f_\mathrm{C}\qty(\bar{\vb*{a}}, \bar{\vb*{u}}) = \bar{\vb*{f}}\qty(\bar{\vb*{a}}) \cdot \bar{\vb*{u}} \] で定義されていました(\(f\) と \(\bar{\vb*{f}}\) を混同しやすいので、コンプライアンスを表す C を付記しました)。
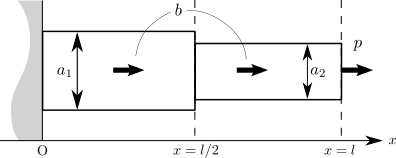
以降で Lagrange 乗数法に基づいてコンプライアンスの感度を求めますが、表記の簡略化のために \(\bar{\vb*{K}}\qty(\bar{\vb*{a}})\) や \(\bar{\vb*{f}}\qty(\bar{\vb*{a}})\) は単に \(\bar{\vb*{K}}\) や \(\bar{\vb*{f}}\) と書くことにします。
*****
さて、まずは前回の記事で紹介した Lagrange 乗数法の考え方に倣って Lagrange 関数を定義しましょう。 ここでの制約条件は状態方程式、すなわち式 \((1)\) となります。 これは2変数の連立1次方程式となるので、等式制約が2つあることを表します。 そこで Lagrange 乗数を2次元ベクトル \(\bar{\vb*{v}} = (v_1, v_2)^\mathsf{T}\) として用意し、式 \((1)\) の各行がイコールゼロとなるように変形したもの(\(-\bar{\vb*{K}}\bar{\vb*{u}} + \bar{\vb*{f}}\))と \(\bar{\vb*{v}}\) の各成分の積を足して、Lagrange 関数は \[ \mathscr{L}\qty(\bar{\vb*{a}}, \bar{\vb*{u}}, \bar{\vb*{v}}) = f_\mathrm{C}\qty(\bar{\vb*{a}}, \bar{\vb*{u}}) + \bar{\vb*{v}}\cdot\qty(-\bar{\vb*{K}}\bar{\vb*{u}} + \bar{\vb*{f}}) \] のように定義します。
このとき、コンプライアンスの微分は \(\bar{\vb*{u}}\) に対する Lagrange 関数の停留条件 \[ \pdv{\mathscr{L}}{\bar{\vb*{u}}}\qty(\bar{\vb*{a}}, \bar{\vb*{u}}, \bar{\vb*{v}}) = \vb*{0} \tag{2} \] と \(\bar{\vb*{v}}\) に対する Lagrange 関数の停留条件 \[ \pdv{\mathscr{L}}{\bar{\vb*{v}}}\qty(\bar{\vb*{a}}, \bar{\vb*{u}}, \bar{\vb*{v}}) = \vb*{0} \tag{3} \] が成り立つもとでの、\(\bar{\vb*{a}}\) に対する Lagrange 関数の微分 \[ \pdv{\mathscr{L}}{\bar{\vb*{a}}}\qty(\bar{\vb*{a}}, \bar{\vb*{u}}, \bar{\vb*{v}}) \tag{4} \] で表されます。
式 \((2)\) の左辺を計算すると、 \[ \begin{align} & \pdv{\mathscr{L}}{\bar{\vb*{u}}}\qty(\bar{\vb*{a}}, \bar{\vb*{u}}, \bar{\vb*{v}}) \\ & = \pdv{\bar{\vb*{u}}} \qty(f_\mathrm{C}\qty(\bar{\vb*{a}}, \bar{\vb*{u}}) + \bar{\vb*{v}} \cdot \qty(-\bar{\vb*{K}}\bar{\vb*{u}} + \bar{\vb*{f}})) \\ & = \pdv{f_\mathrm{C}}{\bar{\vb*{u}}} \qty(\bar{\vb*{a}}, \bar{\vb*{u}}) + \pdv{\bar{\vb*{u}}}\qty(\bar{\vb*{v}} \cdot \qty(-\bar{\vb*{K}}\bar{\vb*{u}} + \bar{\vb*{f}})) \\ & = \pdv{f_\mathrm{C}}{\bar{\vb*{u}}} \qty(\bar{\vb*{a}}, \bar{\vb*{u}}) + \bar{\vb*{v}} \cdot \qty(-\bar{\vb*{K}}) \\ & = \pdv{f_\mathrm{C}}{\bar{\vb*{u}}} \qty(\bar{\vb*{a}}, \bar{\vb*{u}}) - \bar{\vb*{K}}^\mathsf{T} \bar{\vb*{v}} \end{align} \] となります。 剛性行列が対称であることを踏まえると、 \[ \bar{\vb*{K}}\bar{\vb*{v}} = \pdv{f_\mathrm{C}}{\bar{\vb*{u}}} \qty(\bar{\vb*{a}}, \bar{\vb*{u}}) \] を満たすように \(\bar{\vb*{v}}\) を定めれば、この項はゼロとなります。 しかし、今回の問題の場合だと \[ \pdv{f_\mathrm{C}}{\bar{\vb*{u}}} \qty(\bar{\vb*{a}}, \bar{\vb*{u}}) = \pdv{\bar{\vb*{u}}}\qty(\bar{\vb*{f}} \cdot \bar{\vb*{u}}) = \bar{\vb*{f}} \] となることから、この方程式は状態方程式とまったく同じ形となることがわかります。 したがって \(\bar{\vb*{v}} = \bar{\vb*{u}}\) とすることで式 \((2)\) の停留条件を満たすことができます。
次に式 \((3)\) の左辺を計算すると、 \[ \begin{align} & \pdv{\mathscr{L}}{\bar{\vb*{v}}}\qty(\bar{\vb*{a}}, \bar{\vb*{u}}, \bar{\vb*{v}}) \\ & = \pdv{\bar{\vb*{v}}} \qty(f_\mathrm{C}\qty(\bar{\vb*{a}}, \bar{\vb*{u}}) + \bar{\vb*{v}} \cdot \qty(-\bar{\vb*{K}}\bar{\vb*{u}} + \bar{\vb*{f}})) \\ & = \pdv{f_\mathrm{C}}{\bar{\vb*{v}}} \qty(\bar{\vb*{a}}, \bar{\vb*{u}}) + \pdv{\bar{\vb*{v}}}\qty(\bar{\vb*{v}} \cdot \qty(-\bar{\vb*{K}}\bar{\vb*{u}} + \bar{\vb*{f}})) \\ & = -\bar{\vb*{K}}\bar{\vb*{u}} + \bar{\vb*{f}} \\ \end{align} \] となります。 これは状態方程式とまったく同じ形をしているため、\(\bar{\vb*{u}}\) が状態方程式の解であればこの項はゼロとなることがわかります。
最後に式 \((4)\) の左辺を計算します。まず \(a_1\) について計算してみると、 \begin{align} & \pdv{\mathscr{L}}{a_1}\qty(\bar{\vb*{a}}, \bar{\vb*{u}}, \bar{\vb*{v}}) \\ & = \pdv{a_1} \qty(f_\mathrm{C}\qty(\bar{\vb*{a}}, \bar{\vb*{u}}) + \bar{\vb*{v}} \cdot \qty(-\bar{\vb*{K}}\bar{\vb*{u}} + \bar{\vb*{f}})) \\ & = \pdv{f_\mathrm{C}}{a_1} \qty(\bar{\vb*{a}}, \bar{\vb*{u}}) + \pdv{a_1}\qty(\bar{\vb*{v}} \cdot \qty(-\bar{\vb*{K}}\bar{\vb*{u}} + \bar{\vb*{f}})) \\ & = \pdv{f_\mathrm{C}}{a_1} \qty(\bar{\vb*{a}}, \bar{\vb*{u}}) + \bar{\vb*{v}} \cdot \qty(-\pdv{\bar{\vb*{K}}}{a_1}\bar{\vb*{u}} + \pdv{\bar{\vb*{f}}}{a_1}) \tag{5} \\ & = \dfrac{1}{4}blu_1 + \bar{\vb*{v}} \cdot \qty(-\dfrac{2E}{l}\mqty(1 & 0 \\ 0 & 0)\bar{\vb*{u}} + \dfrac{1}{4}bl\mqty(1 \\ 0)) \\ & = \dfrac{1}{4}blu_1 - \dfrac{2E}{l} u_1 v_1 + \dfrac{1}{4}blv_1 \\ \end{align} となります。 これまでに求めた停留条件(\(\bar{\vb*{u}}\)、\(\bar{\vb*{v}}\) をともに状態方程式の解とする)を考慮して、\(v_1 = u_1\) とすると、結果として \[ \pdv{\mathscr{L}}{a_1}\qty(\bar{\vb*{a}}, \bar{\vb*{u}}, \bar{\vb*{v}}) = \dfrac{1}{2}blu_1 - \dfrac{2E}{l} u_1^2 \] という式が得られます。 この結果は第23回の記事で求めた直接微分法によるものと一致しています。 同様にして \(a_2\) について計算してみても、直接微分法の結果と同じものが得られます。
*****
さて、なぜ今回のような手順でコンプライアンスの感度が求められたのでしょうか。 ここで第23回の記事で確認した、直接微分法を使ったときの \(a_1\) に対する \(f_\mathrm{C}\) の微分 \[ \dv{f_\mathrm{C}}{a_1} = \pdv{f_\mathrm{C}}{a_1} + \pdv{f_\mathrm{C}}{\bar{\vb*{u}}} \cdot \pdv{\bar{\vb*{u}}}{a_1} \tag{6} \] について見てみましょう。 \(\pdv*{f_\mathrm{C}}{\bar{\vb*{u}}}\) の項は式 \((2)\) の計算過程で確認したように、\(\bar{\vb*{v}}\) を使って \(\bar{\vb*{K}}^\mathsf{T}\bar{\vb*{v}}\) と置き換えることができます。 \(\pdv*{\bar{\vb*{u}}}{a_1}\) の項は第23回の記事でも見たように \[ \pdv{\bar{\vb*{u}}}{a_1} = \bar{\vb*{K}}^{-1}\qty(-\pdv{\bar{\vb*{K}}}{a_1} \bar{\vb*{u}} + \pdv{\bar{\vb*{f}}}{a_1}) \tag{7} \] と置き換えることができます。 これらを代入することで、式 \((6)\) の右辺第2項は \begin{align} & \pdv{f_\mathrm{C}}{\bar{\vb*{u}}} \cdot \pdv{\bar{\vb*{u}}}{a_1} \\ & = \qty(\bar{\vb*{K}}^\mathsf{T}\bar{\vb*{v}}) \cdot \qty(\bar{\vb*{K}}^{-1}\qty(-\pdv{\bar{\vb*{K}}}{a_1} \bar{\vb*{u}} + \pdv{\bar{\vb*{f}}}{a_1})) \\ & = \qty(\bar{\vb*{v}}\cdot\bar{\vb*{K}})\qty(\bar{\vb*{K}}^{-1}\qty(-\pdv{\bar{\vb*{K}}}{a_1} \bar{\vb*{u}} + \pdv{\bar{\vb*{f}}}{a_1})) \\ & = \bar{\vb*{v}}\cdot\bar{\vb*{K}}\bar{\vb*{K}}^{-1}\qty(-\pdv{\bar{\vb*{K}}}{a_1} \bar{\vb*{u}} + \pdv{\bar{\vb*{f}}}{a_1}) \\ & = \bar{\vb*{v}}\cdot\qty(-\pdv{\bar{\vb*{K}}}{a_1} \bar{\vb*{u}} + \pdv{\bar{\vb*{f}}}{a_1}) \end{align} となり、\(\pdv*{f_\mathrm{C}}{a_1}\) と合わせれば式 \((5)\) と一致することがわかります。 つまり、Lagrange 乗数法の枠組みで求めたコンプライアンスの微分は、結局のところ直接微分法で求めたコンプライアンスの微分を別の形で表現しているにすぎないのです。
とは言っても、直接微分法と Lagrange 乗数法にはそれぞれの特徴があります。 今回は設計変数が \(\bar{\vb*{a}} = (a_1, a_2)^\mathsf{T}\) という2次元ベクトルだったので、直接微分法における式 \((7)\) の計算は \(a_1\) と \(a_2\) についての2回分が必要となりました。 これが設計変数の次元がもっと大きくなったときにはそれと同じ回数分の計算が必要となり、計算量が大きく膨れ上がってしまうのです。 ノンパラメトリックな構造最適化の場合、無限次元に相当する設計変数である関数を扱うということを考えると、直接微分法を用いるのは非常に不利であるということがわかるかと思います。
一方で Lagrange 乗数法で求めることになる \(\bar{\vb*{v}}\) の計算には、設計変数の次元は一切関与しません。 \(\bar{\vb*{v}}\) の次元は状態変数 \(\bar{\vb*{u}}\) の次元と一致するので、\(\bar{\vb*{v}}\) の計算量は \(\bar{\vb*{u}}\) の計算量と同等なものとなります。 そういう意味で、ノンパラメトリックな構造最適化においては直接微分法より有利な方法であると言えるのです。
Lagrange 乗数法で現れた \(\bar{\vb*{K}}^\mathsf{T}\bar{\vb*{v}} = \pdv*{f_\mathrm{C}}{\bar{\vb*{u}}}\) という方程式は随伴問題や随伴方程式と呼ばれます。 そしてその解 \(\bar{\vb*{v}}\) は Lagrange 乗数として導入した変数でしたが、ここでは随伴変数とも呼ばれます。 直接微分法の計算過程で式 \((7)\) を評価する代わりに随伴変数を求めることでも同じ結果が得られますが、このアプローチでは Lagrange 関数の定義を必要としないので、随伴変数法と呼んだりもします。
また、上述したように \(\pdv*{f_\mathrm{C}}{\bar{\vb*{u}}}\) が状態方程式の右辺ベクトル \(\bar{\vb*{f}}\) と一致するときは \(\bar{\vb*{v}} = \bar{\vb*{u}}\) という関係が成り立ちます。 状態変数と随伴変数が等しいという関係は自己随伴と呼ばれます。
*****
今回は1次元片持ち梁に対するコンプライアンスの感度について、Lagrange 乗数法を使った導出の考え方を解説しました。 今回までは設計変数を有限次元のベクトルとして問題を構成してきましたが、次回以降はそれと対比しながら、設計変数が関数であるときのコンプライアンスの感度について見ていこうと思います。
★ご意見・ご感想はこちらへ★
![]() https://www.quint.co.jp/cgi-bin/qrepo-impr.cgi
https://www.quint.co.jp/cgi-bin/qrepo-impr.cgi
