第26話 コンプライアンスの感度 その4
「関数で表された設計変数による問題」
前回までの記事で、1次元片持ち梁について2次元の設計変数を導入したときのコンプライアンスとその感度について解説しました。 今回はいよいよ設計変数を有限次元のベクトルから無限次元の関数へと置き換えて問題を構成します。
*****
前回までの記事で扱った問題と比較しながら問題を追いたいので、ここでも1次元片持ち梁を題材とします。 これまでの記事では断面積を2つの実数 \(a_1\)、\(a_2\) として考えていましたが、今回はそれを区間 \((0, l)\) で定義された関数 \(a\) で置き換えることになります。
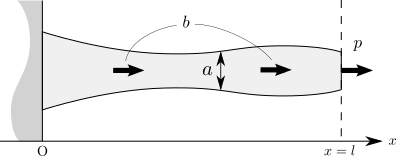
これまで扱った問題と同様にして、このような1次元片持ち梁に物体力 \(b\) と境界力 \(p\) を作用させることを考えます。 このときの変位 \(\require{physics} u\) は、偏微分方程式の境界値問題 \begin{align} -\dv{x}\qty(a\sigma\qty(u)) & = ab \quad &&\mbox{in $(0, l)$}, \\ u & = 0 \quad && \mbox{on $x = 0$}, \\ a\sigma\qty(u) & = p \quad && \mbox{on $x = l$} \end{align} の解として表されます(\(\sigma\qty(\,\cdot\,) = E\varepsilon\qty(\,\cdot\,)\) が応力を、\(\varepsilon\qty(\,\cdot\,) = \dv*{\qty(\,\cdot\,)}{x}\) がひずみを表すのはこれまでと同様です)。 このときコンプライアンスは \[ f_\mathrm{C}\qty(a, u) = \int_{0}^{l} abu \dd{x} + pu\qty(l) \] となります。 第21回の記事と比較するとわかりますが、断面積 \(a\) が所々にかかるような違いが生じます。
*****
続いて、上記の偏微分方程式の境界値問題を弱形式と呼ばれる形に変形しておきます。 有限要素法を学んだことのある方であればなじみのある操作かと思いますが、結果だけ書くと \[ \int_{0}^{l} a \sigma\qty(u) \varepsilon\qty(v) \dd{x} = \int_{0}^{l} abv \dd{x} + pv\qty(l) \tag{1} \] のような積分で表される方程式となります。 ここで導入された \(v\) は試験関数や仮想変位などと呼ばれるもので、\(u\) が上記の問題の解であれば \(v\qty(0) = 0\) を満たすどのような \(v\) に対してもこの式が成り立ちます。
ちなみに、前回までの記事で扱っていた問題の状態方程式は、この弱形式に変位の補間式を代入することで導出されるものとなります。 \(u\) だけでなく \(v\) に対しても同じ式を適用して得られた結果を整理すると、 \[ \bar{\vb*{v}} \cdot \qty(\bar{\vb*{K}} \bar{\vb*{u}}) = \bar{\vb*{f}} \cdot \bar{\vb*{v}} \] という式が得られます。 どのような \(\bar{\vb*{v}}\) に対してもこの式を成り立たせるためには、\(\bar{\vb*{u}}\) が前回までの記事でも出てきたような状態方程式(\(\bar{\vb*{K}}\bar{\vb*{u}} = \bar{\vb*{f}}\))の解である必要があります。 そういうわけなので、式 \((1)\) は前回までの記事でいうところの \(\bar{\vb*{K}}\bar{\vb*{u}} = \bar{\vb*{f}}\) に相当するものとなります。
*****
さて、ここからは Lagrange 乗数法でコンプライアンスの感度を求めるための準備を始めていきます。 はじめに Lagrange 関数の定義を行いますが、これは前回の記事と同じようにして、コンプライアンスの定義に状態方程式 \((1)\) をイコールゼロとなるように変形(移項)したものを足して \[ \mathscr{L}\qty(a, u, v) = f_\mathrm{C}\qty(a, u) + \qty{-\int_{0}^{l} a \sigma\qty(u) \varepsilon\qty(v) \dd{x} + \int_{0}^{l} abv \dd{x} + pv\qty(l)} \tag{2} \] のように定義されます。 この Lagrange 関数を前回の記事で出てきたもの(を少し書き換えた式) \[ \mathscr{L}\qty(\bar{\vb*{a}}, \bar{\vb*{u}}, \bar{\vb*{v}}) = f_\mathrm{C}\qty(\bar{\vb*{a}}, \bar{\vb*{u}}) + \qty{-\bar{\vb*{v}} \cdot \qty(\bar{\vb*{K}}\bar{\vb*{u}}) + \bar{\vb*{f}}\cdot\bar{\vb*{v}}} \] と比べると、同じ構造をしていることがわかりますね。 \begin{align} f_\mathrm{C}\qty(\bar{\vb*{a}}, \bar{\vb*{u}}) & \to f_\mathrm{C}\qty(a, u) \\ -\bar{\vb*{v}} \cdot \qty(\bar{\vb*{K}}\bar{\vb*{u}}) & \to -\int_{0}^{l} a \sigma\qty(u) \varepsilon\qty(v) \dd{x} \\ \bar{\vb*{f}}\cdot\bar{\vb*{v}} & \to \int_{0}^{l} abv \dd{x} + pv\qty(l) \end{align}
前回の記事で \(\bar{\vb*{v}}\) は Lagrange 乗数として導入していましたが、それは今回の問題においても同じです。 つまり、状態方程式の弱形式を導出した段階では \(v\) は試験関数としての役割を持っていましたが、ここでは Lagrange 乗数としての役割も持っているのです。
*****
さて、Lagrange 関数が式 \((2)\) のように定義されたので、コンプライアンスの感度は \(u\) と \(v\) に対する停留条件のもとでの \(a\) に対する微分として計算できます。 しかし今回の問題では \(a\)、\(u\)、\(v\) はすべて関数になっているので、このためにはいわゆる変分法に基づいたアプローチが必要となります。 次回の記事ではその解説から始めたいと思います。
★ご意見・ご感想はこちらへ★
![]() https://www.quint.co.jp/cgi-bin/qrepo-impr.cgi
https://www.quint.co.jp/cgi-bin/qrepo-impr.cgi
