第13話 H1 勾配法とは その6「3つの関数とH1との関係」
前回は関数空間におけるノルムと内積について解説しました。
最後に関数空間の考え方をより深く理解して頂くために、エンジニアリングの分野(例えば、制御工学や振動工学)でよく出てくる 3 つの関数と \(H^{1}\) との微妙な関係を述べておきます。
ランプ関数は \(x \le 0\) の時に \(0\) で、\(x \gt 0 \) の場合 \(x\) となるような関数です。 この関数は \(H^{1}\) に含まれます。 このランプ関数を微分した関数はステップ関数(ヘビサイドの階段関数)と呼ばれ、さらにそれを微分した関数はデルタ関数(ディラックのデルタ関数)と呼ばれます。 逆に、デルタ関数を積分するとステップ関数、ステップ関数を積分するとランプ関数になります。
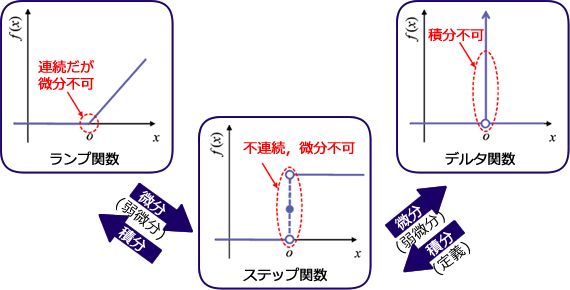
ランプ関数は \(H^{1}\) に含まれる典型的な関数です。これは第8回で説明した通りです。
ステップ関数を微分するとデルタ関数になる、という知識をお持ちのエンジニアは、ステップ関数も \(H^{1}\) に含まれるのではないかと考えがちです。
確かに、ステップ関数の1階微分がデルタ関数で、デルタ関数が無限大にならないで積分できるとすれば、\(H^{1}\) に含まれていても良いような気がしてきます。
正確には \(H^{1}\) のノルムは1階微分の2乗を積分しますので、デルタ関数の2乗が計算できるかどうか、という疑問が湧いてきます。
実は、デルタ関数の2乗は定義されていないので、ステップ関数は \(H^{1}\) に含まれません。
また、デルタ関数自身も \(L^{2}\) に含まれません。
デルタ関数自身が \(L^{2}\) に含まれないとしても、\(L^{1}\) には含まれていて良いような気がする方も多いかと思います。
また、ステップ関数についても \(H^{1}(= W^{1,2})\) には含まれないとしても \(W^{1,1}\) には含まれていて良さそうな気がします。
しかしながら結論から言うと、デルタ関数はいかなるルベーグ空間 \(L^{p}, p = 1, 2, ...\) にも含まれませんし、ステップ関数はいかなるソボレフ空間 \(W^{1,p}, p = 1, 2, ...\) にも含まれません。
この事実は、ステップ関数とデルタ関数の関係をご存知の方には少々衝撃的かもしれませんが、その理由が分かると、ルベーグ空間やソボレフ空間における「積分」やソボレフ空間における「微分」の理解が深まります。
そもそも、ランプ関数は微分可能な関数ではありません。
ランプ関数のグラフを見ると \(x = 0\) のところで傾きが不連続に変化しています。
この部分は数学的に言えば、微分が不可能なのです。
しかしながら、\(x = 0\) の点での微分値が何であろうと、「微分した関数(導関数)の積分」は計算できます。
これは「弱微分」という考え方で、部分積分に基づいて定義されます。
ソボレフ空間の文脈で出て来る「微分」という概念は、正確に言えば、この「弱微分」という概念が使われています。
つまり、ランプ関数の「弱微分」がステップ関数になるのです。
ステップ関数は \(x = 0\) のところで不連続になります。
通常、ステップ関数と言えば \(x = 0\) のところで 0.0, 0.5, 1.0 等になるように定義されますが、\(x = 0\) のところでどんな値をとっても
ランプ関数の「弱微分」になります。
つまりランプ関数の弱微分は一意に決まらず、積分値が一致する範囲で任意性があるのです。
そのような考え方で、さらにステップ関数の「弱微分」として考え出されたものがデルタ関数なのです。 デルタ関数は数学的に言えば「関数」とさえ呼べないもので、普通は「超関数」と呼んで普通の関数とは区別します。 デルタ関数は \(x = 0\) で無限大になり、それ以外では \(0\) になります。 そのため、\(x = 0\) を含む領域で積分すると積分値は \(1\) になりますが、\(x = 0\) を避けるように積分領域を選ぶと積分値は \(0\) となってしまい、矛盾が生じます。 このような状況は、数学的に言えば「積分できない」ということになります。 「デルタ関数の積分はステップ関数になる」というのは、定義だと言っても良いもので、自由自在に積分できるという訳ではないのです。 従って、ルベーグ空間の \(L^{p}\) ノルム(の計算に必要な積分)が計算できないのでルベーグ空間には含まれなくなります。 ステップ関数の弱微分がデルタ関数ですから、ステップ関数の1階微分に関するノルムは一切計算できない、ということですからステップ関数はルベーグ空間には含まれるものの \(H^{1}\) や \(W^{1,1}\) には含まれないということになります。 同様にランプ関数は \(H^{1}\) に含まれますが \(H^{2}\) には含まれません。
デルタ関数はイギリスの理論物理学者ポール・ディラックに因んで「ディラックのデルタ関数」あるいは正確には関数ではないので「ディラックのデルタ」等と呼ばれます。 上記のように「デルタ関数はルベーグ空間に含まれない」と聞くと「物理学者の考えたことは数学者のお気に召さなかったのか。。。」と考えてしまいますが、デルタ関数は典型的な超関数であり、超関数論は数学の世界でも受け入れられて様々な分野に応用されています。
*****
第8回からこの記事まで、\(H^{1}\) 勾配法の「\(H^{1}\)」に焦点を当てて解説しました。 長くなりましたので、ここまでの話をまとめておきます。
\(H^1\) 勾配法の \(H^1\) とは、ある種の関数空間を表すのでした。
空間とは集合の概念に似たもので、その元の間になんらかの関係性が定まっているものを集めたものでした。
その例として、元同士の線形結合が定義された線形空間、距離が定義された距離空間、大きさを一般化した概念であるノルムが定義されたノルム空間、内積が定義された内積空間を紹介しました。
距離が定義されていれば、その空間におけるコーシー点列を考えることができました。 これは互いの距離がゼロに収束するような点の並びでした。 いかなるコーシー点列でも同じ空間上に収束するという性質を完備性と呼ぶのでした。 この性質は距離空間における連続性と考えることができるものでした。 そして、完備な内積空間をヒルベルト空間と呼ぶのでした。
関数空間として、関数そのものを用いたノルムが定義されたルベーグ空間と、さらにその導関数を取り入れたノルムが定義されたソボレフ空間を紹介しました。 \(H^1\) とはソボレフ空間の一種で、関数同士の内積が定義された関数空間となっていました。 そして、この関数空間は完備であることにも触れました。 つまり、\(H^1\) に属する関数の点列が収束するならば、その収束点も \(H^1\) の元となることが保証されているのでした。
*****
次回からは「勾配法」とはどのようなものか、その中で \(H^{1}\) の性質がどのように役立つのかについて、解説していきたいと思います。
★ご意見・ご感想はこちらへ★
![]() https://www.quint.co.jp/cgi-bin/qrepo-impr.cgi
https://www.quint.co.jp/cgi-bin/qrepo-impr.cgi
