第12話 H1 勾配法とは その5「無限次元と関数空間」
前回は空間の完備性について解説しました。 \(H^{1}\) は関数空間ですから、\(H^{1}\) について理解を深めて頂くために今回は関数空間におけるノルムや内積について解説します。
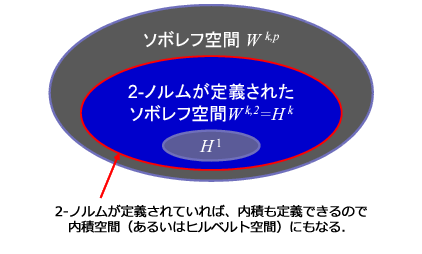
第8回でも述べましたが、ここで改めて \(H^{1}\) について説明しておきます。
\(H^{1}\) はソボレフ空間の記号で \(W^{1,2}\) とも書きます。
これは関数それ自体と1階の導関数の \(L^{2}\) ノルム(2-ノルム)が定義されている(無限大にならない)関数からなる完備なベクトル空間のことです。
\(H^{1}\) は線形空間ですから、関数同士の和を計算できるように定義域と値域が揃った関数だけで考える必要があります。 ここでは簡単に 0 以上1 以下の実数を定義域とし、実数全体を値域とする関数 \(f\) について考えることにします。
まず、\(f\) の簡単なノルムを定義してみましょう。 前回述べた \(p\) -ノルムの関数版は、次のように定義できます。 \[ \|f\|_{L^p} \equiv \left( \int_{0}^{1} |f(x)|^{p} \,dx \right)^{1/p} \] このようなノルムが定義された関数空間は「\(L^{p}\) 空間」あるいはフランスの数学者 Henri Leon Lebesgue に因んで「ルベーグ空間」と呼ばれます。 ルベーグ空間に入る関数は、このように定義されたノルムが有限の値となる(ルベーグ可積分である)ことが求められます。
ソボレフ空間は、ルベーグ空間の考え方を拡張して、関数そのものに加えてその導関数(微分)を取り入れたノルムが定義された空間です。
例えば \(W^{1,p}\) のノルムは次式のように定義されます。
\[
\|f\|_{W^{1,p}} \equiv \left( \int_{0}^{1} |f(x)|^{p} \,dx
+ \int_{0}^{1} \left| \dfrac{df(x)}{dx} \right|^{p} \,dx \right)^{1/p}
\]
また、\(W^{2,p}\) の場合はさらに項が増えて次式のようになります。
\[
\|f\|_{W^{2,p}} \equiv \left( \int_{0}^{1} |f(x)|^{p} \,dx
+ \int_{0}^{1} \left| \dfrac{df(x)}{dx} \right|^{p} \,dx
+ \int_{0}^{1} \left| \dfrac{d^{2}f(x)}{dx^{2}} \right|^{p} \,dx \right)^{1/p}
\]
\(H^{1}\) は \(W^{1,2}\) ですから、\(H^{1}\) におけるノルムの定義を具体的に書くと次式のようになります。
\[
\|f\|_{H^{1}} \equiv \left( \int_{0}^{1} |f(x)|^{2} \,dx
+ \int_{0}^{1} \left| \dfrac{df(x)}{dx} \right|^{2} \,dx \right)^{1/2}
\]
よって、この式は1階微分までの項を含む 2-ノルムになっていることが分かります。
2-ノルムですから、そのノルムを付随するような内積が定義できます。
\(f\) と同じ定義域・値域を持つ関数 \(g\) を使って、\(f\) と \(g\) の内積は次式のように定義できます。
\[
\left( f, g \right)_{H^{1}} \equiv \int_{0}^{1} f(x) g(x) \,dx
+ \int_{0}^{1} \dfrac{df(x)}{dx} \dfrac{dg(x)}{dx} \,dx
\]
以上のように定義されたノルムと内積を使って、関数 \(f\)、\(g\) という一見幾何学とは無縁なもの同士の距離や角度がそれぞれ次式のように計算できるようになります。 \[ \begin{align*} & d_{H^{1}}(f, g) \equiv \|f - g\|_{H^{1}} \\ & \cos\theta \equiv \dfrac{\left( f, g \right)_{H^{1}}}{\|f\|_{H^{1}} \|g\|_{H^{1}}} \end{align*} \]
\(H^{1}\) の完備性についても触れておきます。
前回の記事で述べたように、有理数のような抜けのある数ではなく実数を取り扱う限りは、有限次元の空間は完備です。
ところが、関数空間では完備でない空間が有り得ます。
一例として、関数 \(f\) が「連続関数」つまり \(C^{0}\) だとした場合に、連続関数が完備ではないことを示します。
連続関数の集合はそれ自体で加算もスカラー倍も定義できますからベクトル空間になります。
さらに、次のような単純な 2-ノルムを定義することもできますから \(L^{2}\) 空間であると言えます(2-ノルムが無限大になるような関数は予め排除しておく必要はあります)。
\[
\|f\|_{L^2} \equiv \left( \int |f(x)|^{2} dx \right)^{1/2}
\]
ついでに、このようなノルムを付随するような内積や、このノルムに付随する距離もそれぞれ次のように定義できます。
\[
\begin{align*}
& \left( f, g \right)_{L^2} \equiv \int f(x) g(x) dx \\
& d_{L^2}(f, g) \equiv \|f - g\|_{L^2}
\end{align*}
\]
つまり、「連続関数の集合」は立派な内積空間になります。
ところが、この空間は完備性がありません。
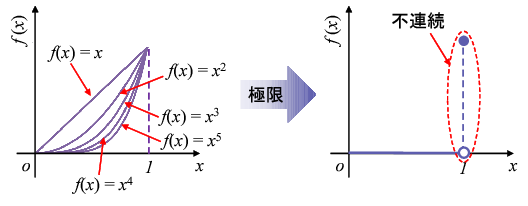
次のような関数列(関数空間上の点列)\(f_{1}(x), f_{2}(x), f_{3}(x), ...\) を考えてみましょう。
\[
f_{n}(x) \equiv x^{n}\ , \quad (n = 1, 2, ...)
\]
この関数列に含まれる関数は全て連続関数ですから、今考えている関数空間に全て含まれます。
これらの関数は \(n\) が大きくなると \(x = 1\) では1に留まりますが、\(0 \le x \lt 1\) の範囲で 0 に近づきますので、次式が成立することが分かります。
\[
\lim_{m, n\to \infty} d_{2}(f_{m}, f_{n}) = 0
\]
従って、この関数列はコーシー点列になります。
ところが、この関数列の \(n \to \infty\) での極限は \(0 \le x \lt 1\) の範囲で 0、\(x = 1\) で1となる不連続関数に収束します。
つまり「コーシー点列の極限がその空間に収まらない(場合がある)」ということは今考えている「連続関数の集合」という空間は「完備ではない」ということになるのです。
同じ「連続関数の集合」を、単純な 2-ノルムの代わりに \(H^{1}\) のノルム(とそれに付随する距離)を使って考えてみましょう。 \(H^{1}\) のノルムが無限大になってしまうような関数は除外しておくことにします。 その上で、関数列 \(f_{1}(x), f_{2}(x), f_{3}(x), ...\) を考えてみましょう。
\(H^{1}\) のノルムや距離の定義には1階微分の項が含まれます。 \(f(x) \equiv x^{n}\) の1階微分は \(f'(x) = nx^{n-1}\) ですから、特に \(x = 1\) の近傍では \(n\) が大きくなるとそれに比例して大きな値になり、収束しません。 従って、\(H^{1}\) の距離 \(d_{H^{1}}(\cdot , \cdot )\) を使って考えると、関数列 \(f_{1}(x), f_{2}(x), f_{3}(x), ...\) は収束しないため、コーシー列にもなりません。 \[ \lim_{m, n\to \infty} d_{H^{1}}(f_{m}, f_{n}) \ne 0 \] そのため、この関数列を考える限りは完備性を確認することすらできません。 この事実だけでは \(H^{1}\) の距離関数を使うと連続関数の集合は完備になる、とまでは言い切れませんが、実際、第8回の記事で述べたように連続関数の中で一部の不都合な関数を除いた集合は \(H^{1}\) になり、完備性があります。 あるいは \(H^{1}\) のノルムが計算できる(無限大にならない)関数だけを集めると自然に完備な空間になる、と言っても構いません。
以上のように完備性は距離の定義と密接な関連がありますので、一般論として、同じ集合であっても距離の定義を変えると完備性の有無も変わる可能性があることに注意が必要です。
*****
次回は関数空間の考え方をより深く理解していただくために、エンジニアリングの分野でよく出てくるランプ関数、ステップ関数、デルタ関数と \(H^1\) との関係について解説します。 また、何回かに分けて続いた関数空間の解説も次回で最後となりますので、これまでの話をまとめておきたいと思います。
★ご意見・ご感想はこちらへ★
![]() https://www.quint.co.jp/cgi-bin/qrepo-impr.cgi
https://www.quint.co.jp/cgi-bin/qrepo-impr.cgi
