第11話 H1勾配法とは その4「完備性」
前回の記事ではノルム空間と内積空間について解説しました。
ノルム空間は大きさの概念を一般化したノルムが備わった空間であり、内積空間は内積が備わった空間でした。
この記事ではこれらの空間の性質の中でも重要な完備性について解説します。
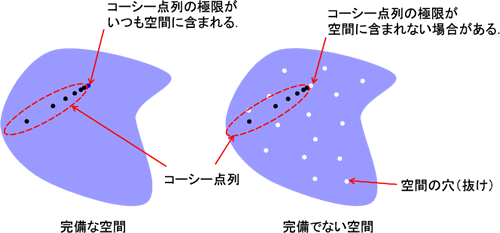
内積空間の中で、特に「完備」という性質(完備性)を持ったものが第8回で説明した「ヒルベルト空間」です。 完備性は微分や積分のような議論を行うにあたって重要な概念です。 微分や積分では距離がゼロになるような極限の操作を行いますが、そのような極限が空間の中に収まっているかどうかを保証するのが完備性です。
「完備」という概念は「実数と何か?」「実数の連続性とは?」「実数と有理数の違いは?」といった、数学のかなり根本的な議論の中で出てくるもので、工学系のエンジニアにはあまり馴染みが無いと思います。 完備性の有無を端的に表す例は「実数全体」と「有理数全体」です。 いずれも内積まで含めて各種の演算が可能な空間なのですが、「実数全体」は完備で、「有理数全体」は完備ではありません。
例えば、無理数である \(\sqrt{2}\) は、実数には含まれますが、有理数ではありません。 ところが、その \(\sqrt{2}\) に限りなく近い有理数は考えることができます。 有理数の中で限りなく \(\sqrt{2}\) に近づくことができるにも関わらず、その \(\sqrt{2}\) 自体は有理数ではない、というのが完備ではない状態なのです。 「実数全体」には \(\sqrt{2}\) などの無理数も含まれますから「有理数全体」のような抜けと言うか隙間と言うか穴のようなものがありません。 要するに、完備性とはそのような空間の抜け、隙間、穴のようなものが無いことを表す概念なのです。
実数や有理数以外でも距離空間(ノルム空間、内積空間もそれらに付随する距離を使って)であれば、「コーシー点列」というものを使って完備性を調べることができます。 「コーシー点列」は互いの距離がゼロになって行くような点の並びです。 空間上の点 \(a_{1}, a_{2}, a_{3}, \dots\) が次式のように互いの距離 \(d(\,\cdot\, , \,\cdot\, )\) がゼロに近づいていく時に、これらの点の並びを「コーシー点列」と言います。 \[ \lim_{m, n \to \infty} d(a_{m}, a_{n}) = 0 \] 空間に含まれるコーシー点列は無数に定義できますが、それらの極限 \(\lim_{n \to \infty}a_{n}\) がいつも空間に含まれる場合を完備だと言います。 逆に極限が空間に含まれないコーシー点列が一つでもあれば、その空間は完備ではありません。
先ほど説明した実数と有理数の話に戻りましょう。
「実数全体」と「有理数全体」はいずれも距離空間でもありますからコーシー点列が定義できます。
例えば、次のような数列を考えてみましょう。
\[
\begin{align}
&a_{1} = 1 \\
&a_{2} = 1.4 \\
&a_{3} = 1.41 \\
&a_{4} = 1.414 \\
&a_{5} = 1.4142 \\
&a_{6} = 1.41421 \\
&a_{7} = 1.414213 \\
&a_{8} = 1.4142135 \\
&\cdots \\
\end{align}
\]
これらの互いの距離 \(d(a_{m}, a_{n}) \equiv |a_{m} - a_{n}|\) は \(m, n \to \infty\) の極限でゼロになりますから、この数列は「実数全体」と「有理数全体」のどちらの観点でもコーシー点列だと言えます。
この数列の極限は \(\sqrt{2}\) なので、実数ですが有理数ではありません。
従って、このコーシー点列は有理数の中で収束しない、つまり有理数は完備ではない、と言うことができるのです。
このように、距離空間であればコーシー点列を使うことで完備性を調べることができるのですが、少なくとも有限次元の空間では、完備性はそれほど厄介なものではありません。 1次元空間の場合は、上で述べたように有理数のようなものではなく、実数を取り扱っている限りは完備性があります。 2次元以上の有限次元ベクトルや複素数であっても、各成分がそれぞれ実数であれば完備性に問題は生じません。 ただ、無限次元の関数空間の場合は定義域と値域が単純な実数であっても完備でない空間が考えられます。 その例については次回解説します。
少し余談ですが、空間そのものではなく、空間の部分集合についての完備性を考える場合は、閉集合か開集合かに注意する必要があります。
例えば、実数全体に対して「0から100までの実数」という部分集合を考えると、その境界である0や100がその部分集合に含まれる場合(\(0 \le x \le 100\), つまり閉集合の場合)は完備ですが、0や100が含まれない場合(\(0 \lt x \lt 100\), つまり開集合の場合)は完備ではありません。
0 や 100 に限りなく近い実数があるにも関わらず、開集合では 0 や 100 そのものはその集合に含まれないので、完備ではないのです。
ちなみに、完備な距離空間は「コーシー空間」、完備なノルム空間は「バナッハ空間」と 呼ばれます。 これらはそれぞれ、フランスの数学者 Augustin Louis Cauchy とポーランドの数学者 Stefan Banach に因んで名付けられています。
以上のように、完備な内積空間であるヒルベルト空間は極限の操作や各種の幾何学的な概念が適用できるという意味で理想的な空間であることが分かります。 また、エンジニアが普通に考える2次元空間や3次元空間(ユークリッド空間とも呼ばれます)を無限次元まで拡張した概念がヒルベルト空間だと言うこともできます。
*****
次回は無限次元の各種空間を解説し、\(H^{1}\) についての理解を深めて頂きます。
★ご意見・ご感想はこちらへ★
![]() https://www.quint.co.jp/cgi-bin/qrepo-impr.cgi
https://www.quint.co.jp/cgi-bin/qrepo-impr.cgi
