第10話 H1勾配法とは その3「ノルム空間と内積空間」
前回の記事では、現代数学における「空間」という概念について解説しました。
「特定の何かを集めたもの」として集合という概念が存在し、その中でもそれに属する元同士になんらかの関係性を決めることができるものを特に「空間」と呼ぶのでした。
また、具体的な空間の例として「線形空間」と「距離空間」を紹介しました。
この記事ではさらに話を進めて、ノルムや内積が定義された空間について解説します。
「ノルム」とはベクトルの大きさ(あるいは長さ、絶対値)を一般化した概念です。 \(\|\, \cdot \,\|\) という記号で表記します。 2次元実ベクトル \(v = (x,y)\) のノルムを考えてみましょう。 通常、ベクトルの大きさは次のような計算で求められます。 \[ \|v\|_{2} \equiv (x^{2} + y^{2})^{1/2} \] これは立派な2次元ベクトルの「ノルム」の定義であり、「ユークリッドノルム」あるいは「2 - ノルム」と呼ばれます。
勘の良い方なら分かると思いますが、上の式の「2」は他の数字に置き換えても「ノルム」の定義として使えます。 一般的に、「\(p\)」という文字を使って、 \[ \|v\|_{p} \equiv (|x|^{p} + |y|^{p})^{1/p} \] と定義することができ、このようなノルムは「\(p\) - ノルム」と呼ばれます。 距離空間における距離の定義のように、ノルムの定義には一定のルールがあります。 上の式では \(1 \le p \le \infty \) の範囲であればノルムの定義として使えます。 \(p = \infty\) の場合は難しそうに思えますが、これは「\(|x|\) と \(|y|\) のどちらか大きい方の値」という意味になります。 つまり、式で書くと次式のようになります。 \[ \|v\|_{\infty} \equiv \max (|x|,|y|) \] この場合のノルムは「無限大ノルム」あるいは「最大値ノルム」と呼ばれます。
以上のように、単に2次元ベクトルのノルムと言っても様々な定義が考えられることがお分かり頂けるでしょう。 ノルムは2次元ベクトルだけでなく、1次元でも、無限次元の関数空間でも定義できます。 関数空間のノルムについては以降の回で改めて解説します。 ノルムが定義された線形空間は「ノルム線形空間」あるいは単に「ノルム空間」と呼ばれます。 ノルム空間は線形空間でもあるので、「差」を計算することができます。 その「差」のノルムは「距離」の定義に使えますから、ノルム空間は全て距離空間でもあります。
一方、「内積」とは2つのベクトルの間の角度を得るために必要な概念です。
2次元ベクトル \(v_{1} = (x_{1}, y_{1})\) と \(v_{2} = (x_{2},y_{2})\) の内積を考えてみましょう。
通常、内積と言うと次のような演算を思い浮かべる方が多いでしょう。
\[
v_{1} \cdot v_{2} \equiv x_{1} x_{2} + y_{1} y_{2}
\]
この演算は点乗積、ドット積と呼ばれるもので、勿論これは内積の定義として十分に通用しますが、内積の定義はこれだけではありません。
例えば、それぞれの項に重み係数 \(w_{1}\)、\(w_{2}\) を付けて、
\[
\langle v_{1},v_{2} \rangle \equiv w_{1} x_{1} x_{2} + w_{2} y_{1} y_{2}
\]
としても構いません。
上式のように内積は通常 \(\langle \,\cdot\, , \,\cdot\, \rangle\) と表記されます。
上式で \(w_{1}, w_{2}\) が両方とも正の値であれば、内積の定義として使えます。
さらにもっと一般的に、2行2列の実対称行列 \([A]\) を使って、
\[
\langle v_{1},v_{2} \rangle \equiv \{ v_{1} \}^{\mathsf{T}} [A] \{ v_{2}\}
\]
と定義しても構いません。
\([A]\) が正定値行列であれば、内積の定義として使えます。
このように、ノルムと同様に内積の定義も様々なものが考えられます。
また、2次元ベクトル以外にも1次元から無限次元の関数空間まで、それぞれ内積を定義することができます。
ところで、点乗積の定義と2-ノルムの定義が似ていることにお気付きでしょうか?
2つの同じベクトル \(v\) の点乗積の1/2乗は、ちょうど2-ノルムになります。
つまり、
\[
(v \cdot v)^{1/2} = (|x|^{2} + |y|^{2})^{1/2} = \|v\|_{2}
\]
が成り立ちます。
一般的に言えば、内積が定義できればそれを使ってノルムも定義することができます。
そのようなノルムは「内積に付随するノルム」等と呼ばれます。
内積とそれに付随するノルムの関係は次のように表すことができます。
\[
\|v\| \equiv \langle v, v {\rangle}^{1/2}
\]
内積とそれに付随するノルムが定義できれば、それらを使って「角度」を計算することができます。
2つのベクトルの角度 \(\theta\) は次式で計算できます。
\[
\cos\theta = \dfrac{\langle v_{1},v_{2} \rangle }{\|v_{1}\| \ \|v_{2}\|}
\]
同じ2つの2次元ベクトルであっても、内積の定義が変われば2つのベクトルの角度 \(\theta\) は違った値になるので注意が必要です。
つまり現代数学では、角度というのは内積(とそれに付随するノルム)に付随して定義されるものであって、何か絶対的に決まるものではないのです。
\(\|v_{1}\|\) と \(\|v_{2}\|\) が共に非ゼロにもかかわらず、内積 \(\langle v_{1},v_{2} \rangle\) がゼロの場合、\(v_{1}\) と \(v_{2}\) は「直交」していると言います。 例えば、エンジニアリングの分野で「固有振動モードは互いに直交している」と言いますが、これは数学的に言えば、固有振動モード同士で何らかの内積が定義されていて、その内積が異なる固有振動モードの間ではゼロになる、ということを意味しているのです。
以上のように、内積が定義されれば、それに付随してノルムが定義され、さらにそれに付随して距離や角度が定義されます。 従って、内積が定義されれば、エンジニアが普通に考える2次元空間や2次元空間の幾何学的な概念の多くが適用できることになります。 内積が定義された空間は「内積空間」と呼ばれます。 また、内積空間は距離や角度が定義できることから「計量ベクトル空間」とも呼ばれます。
今回はノルム空間と内積空間について解説しました。 内積空間では内積が定義されており、それに付随するノルムを定義できることから内積空間はノルム空間になるのでした。 また、ノルムが定義できれば2つの元の差のノルムを距離の定義として使えることから、ノルム空間は距離空間にもなるのでした。 したがって、これら3つの空間の関係をイメージとして描くと下図のようになります。
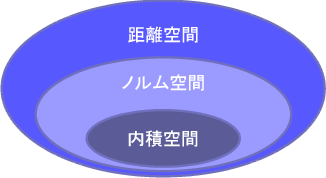
*****
次回はノルムを用いて調べることができる、空間の完備性という性質について解説します。
この性質は \(H^1\) 勾配法を理解する上で非常に重要なものとなります。
★ご意見・ご感想はこちらへ★
![]() https://www.quint.co.jp/cgi-bin/qrepo-impr.cgi
https://www.quint.co.jp/cgi-bin/qrepo-impr.cgi
