第9話 H1勾配法とは その2「空間」
前回の記事では、\(H^{1}\) という関数空間についての概要を述べました。
その中で少し述べましたが、エンジニアが考える「空間」と現代数学における「空間」には大きな違いがあります。
今回は現代数学における「空間」の概念について解説します。
数学における「空間」という概念は「集合」の一つとして位置づけられています。
いずれも「特定の何かを集めたもの」という意味がありますが、それに属する元(要素)同士になんらかの関係性を決めることができるものを特に「空間」と呼びます。
例えばエンジニアの方にもお馴染みの3次元空間は3次元の座標点 \((x, y, z)\) を全て集めた集合ですが、2つの点の和やスカラー倍などの演算を考えることができるため、「空間」と呼ばれます。
以下では、具体的な空間の例として「線形空間」と「距離空間」について解説します。
ある集合に属する任意の元の線形結合(和およびスカラー倍)が定義されていて、さらにそれらの演算が結合律、可換律、分配律などの幾つかのルールを満足する場合、その集合は「線形空間」あるいは「ベクトル空間」と呼ばれます。 「線形空間」と「ベクトル空間」は何か違うもののような印象を持ってしまいますが、数学的に全く同じ意味です。 先ほどの3次元空間は線形空間の例となります。 その他にも「全ての4次元実ベクトル」、「全ての2行2列の実行列」などはいずれも線形空間です。 また線形空間と言った場合は、任意の元同士の和やスカラー倍の結果がもとの空間に含まれている必要があります。 どのような2つの実数の和やスカラー倍でも実数となるので「実数全体」は線形空間です。 「0以上100以下の実数全体の集合」の元である 60 と 70 の和は 130 となり元の空間の要素ではなくなってしまうので、「0以上100以下の実数全体の集合」は線形空間ではありません。 この場合は空間という言葉を使わずに「部分集合」のように呼ばれます。 このように全体では空間と呼ばれるものであっても、その一部だけを取り出すと空間としての性質が失われる場合があります。
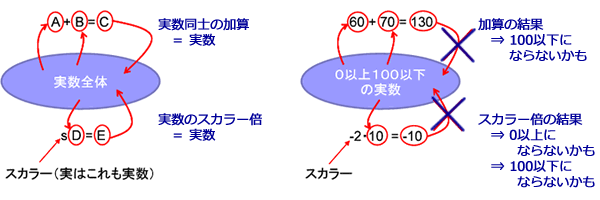
ここで少し余談ですが、「ベクトル空間」の「ベクトル」は、エンジニアが考える「ベクトル」ではなく、空間の元のことを表します。 したがって実数全体の集合も複素数全体の集合も、和とスカラー倍が定義されていますので、線形空間(ベクトル空間)と呼ばれます。 定義域と値域が揃っている関数同士の和や関数のスカラー倍も考えることができますから、そのような関数の集合も線形空間(ベクトル空間)に成り得ます。
また、「線形空間」の「線形」という言葉も、エンジニアが考える線形、非線形とは少し異なります。 構造解析の分野で大変形や塑性変形を考慮した解析を線形弾性解析と区別して「非線形解析」と言いますが、 この「非線形」は変位ベクトルと荷重ベクトルの関係に線形性が成立しないという意味です。 変位ベクトル自体は加算もスカラー倍も通常のベクトル計算と同じ意味で可能ですから、変位ベクトルの集合は線形空間となります。 実際、非線形解析の各種解法は線形空間の性質を当然のように利用しています。
最も基本的な空間の分類の一つに「距離空間」というものがあります。
これは、その空間に含まれる2つの元の間で「距離」が計算できる、という性質を持つものの集合です。
あるいは単純に「距離が定義されている」と言っても良いでしょう。
「距離」には以下のような一定のルールがありますが、その上で自由に定義することができます。
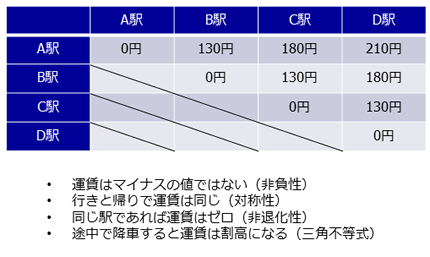
- 非負性
⇒ 距離はマイナスの値になってはいけない - 対称性
⇒ AからBまでの距離とBからAまでの距離は同じでなければならない - 非退化性
⇒ 同じものの間の距離はゼロで、距離がゼロなら同じものでなければならない - 三角不等式
⇒ AからBまでの距離とBからCまでの距離の和は、AからCまでの距離以上でなければならない
例えば整数や実数、複素数の場合は、「差の絶対値」を距離と定義して構いません。 3次元空間上の任意の2点間の距離は通常の距離(ユークリッド距離)の定義をそのまま使うことができます。 関数同士の距離は、例えば関数同士の差の絶対値を定義域で積分すると良いでしょう。 上で述べたように、実数、複素数、有限次元のベクトル、関数はそれぞれ線形空間に成り得ます。 線形空間であれば「差」つまり減算が定義されているので、距離の定義にその減算が利用できるのです。
「JR 東日本の全ての駅」は線形空間ではありませんが距離の定義ができるため、距離空間に成り得ます。 駅の距離は地図上の直線距離でも構いませんし、「駅から別の駅に辿り着くために必要な最小の運賃」を距離と定義しても構いません。
「株式会社くいんとの全ての社員」も距離空間として考えることが可能です。 株式会社くいんとの社員間の距離は、意味があるかどうかはともかく、例えば「社員の身長の差の絶対値」とか「両目の視力の合計値の差の絶対値」等々、いろいろな定義が考えられます。 厳密に言えば、全く同じ身長の人が二人以上いる場合は上で述べた「非退化性」の条件に反するので距離の定義に身長を使うことはできません。 両目の視力の合計値も同様です。
いずれにしても、何らかの距離を定義すると「JR 東日本の全ての駅」や「株式会社くいんとの全社員」という一見幾何学とは無縁の集合に距離という幾何学的な性質を導入した空間になるのです。
このように、現代数学では「距離」というものは何か自然に決まるようなものではなく、人間が一定のルールの下で勝手に定義するものだと考えるのです。
そして、その距離がうまく定義された集合は距離空間と呼ばれるのです。
以上のように、数学で取り扱う空間という概念は、エンジニアが普通に考える2次元空間や3次元空間とはかなり趣が異なるということがお分かり頂けたのではないでしょうか。 普通の2次元空間や3次元空間の幾何学を他のいろいろなものに広く適用できるように拡張された概念が現代数学における空間なのです。 和やスカラー倍、距離の定義に加えて、大きさ(ノルム)や角度(内積)が定義されると、空間としての利用価値が高まります。
*****
次回はノルムや内積が定義される空間について解説します。
★ご意見・ご感想はこちらへ★
![]() https://www.quint.co.jp/cgi-bin/qrepo-impr.cgi
https://www.quint.co.jp/cgi-bin/qrepo-impr.cgi
