第8話 H1勾配法とは その1「そもそも H1 とは?」
前々回と前回の記事で、形状最適化とトポロジー最適化における \(H^{1}\) 勾配法がどのようなものか、歴史的な背景も交えて説明しました。 この記事では \(H^{1}\) 勾配法の「\(H^{1}\)」とは何なのか、解説していきます。
\(H^{1}\) とは数学の記号の一つです。
数学系の学科出身の方はともかく、工学系のエンジニアの方が \(H^{1}\) の概念を理解するのはなかなか難しいかもしれません。
しかしながら「OPTISHAPE-TS に使われている最適化アルゴリズムは何か?」と問われれば「\(H^{1}\) 勾配法です。」と答えるのですが、
そうすると必ず「\(H^{1}\)って何?」と訊かれることになります。この質問はもはや OPTISHAPE-TS の FAQ の一つと言えるでしょう。
この記事では、普通のエンジニアの方でも分かるように、数式は使わずに \(H^{1}\) についての概要を説明していきます。
\(H^{1}\) は関数空間の一つです。
ただ「空間」という言葉のニュアンスが、既に数学者とエンジニアの間で物凄く違います。
エンジニアが「空間」と言うと、例えば『二次元空間』や『三次元空間』、あるいは自動車の車室内空間と言うと
『広がりを持ったものや物事を考える上での基盤になるもの』を連想します。
しかし現代数学では、『ある性質を持ったものを集めたもの』というニュアンスになります。
従って、「関数空間」と言っても何も恐れることはありません。「関数を集めたもの」と言っているに過ぎません。
ただし、単純に何かを集めたものを数学者は「集合」と言います。
数学者にとって、「集合」と「空間」は似た概念なのですが、「空間」と言った場合は「ある性質を持ったものだけを」集めたもの、というニュアンスがあります。
従って、「関数の集合」ではなく「関数空間」と言った場合は、『ある性質を持つ関数だけを集めたもの』と理解すれば良いのです。
そうすると、あとは「どんな性質を持つ関数なのか?」ということを理解するだけです。
\(H^{1}\) に含まれる関数は \(C^{0}\) 連続です。
有限要素法を過去に勉強されたエンジニアの中には \(H^{1}\) には馴染みが無くても「\(C^{0}\)」と言うと理解できる方が多くいらっしゃいます。 \(C^{0}\) は関数の連続性に基づく分類で、ゼロ階微分(つまり関数そのもの)が連続であるような関数を表します。 \(H^{1}\) という関数空間に含まれる関数は \(C^{0}\) の連続性があります。 エンジニアの方が \(C^{0}\) の関数だと言った時に思い浮かべる関数は、概ね \(H^{1}\) に含まれると言って良いでしょう。
\(H^{1}\) の \(H\) はヒルベルト空間を表します。
ヒルベルト空間は、ドイツの数学者 David Hilbert の名前に因んで名付けられた空間です。
ヒルベルト空間を一言で説明すると「内積が定義された完備な空間」ということになります。
「完備」というのは、これも数学の用語なのですが、ひとまず説明は後回しにします。
「内積が定義された」という言葉も、エンジニアには物凄く違和感があると思います。
「内積」と言うと、二次元ベクトル同士の内積や三次元ベクトル同士の内積はすぐに思いつくでしょう。
実際、普通のエンジニアが二次元空間や三次元空間と言って思い浮かべるものは、そういった内積が計算できるという意味で
ヒルベルト空間の一つだと言えるのです。
エンジニアは、内積を『ある決まった計算の方法』だと考えますが、現代の数学者は、『(一定のルールの下で)勝手に定義するもの』だと考えます。
実は、関数同士の内積も定義ができます。前述のとおり「\(H^{1}\)」は関数空間の一つですから、『互いに内積が計算できる関数だけを集めたもの』と理解できます。
唐突に「内積」という言葉が出てくること自体も、エンジニアには違和感があることでしょう。 「内積が定義された」空間に含まれる関数は、数学者から見ればいろいろな事ができるので都合が良いのです。
ここまでの説明を読むと「\(H^{1}\) 勾配法とはヒルベルト空間の勾配法である」と言ってしまいそうになります。 しかしながら、ヒルベルト空間というのは普通の二次元空間や三次元空間から関数空間までを含む非常に幅広い概念ですから、 \(H^{1}\) 勾配法の説明としてはほとんど意味をなしていないことがお分かり頂けるでしょう。
\(H^{1}\) の「1」は1階微分を表します。
実は、「\(H^{1}\)」という記号は、ヒルベルト空間の記号と言うよりは、むしろソボレフ空間の記号の一つなのです。
ソボレフ空間はロシアの数学者 Sergei Sobolev に因んで名付けられた空間で、関数空間の一つです。
ソボレフ空間は、通常「\(W\)」という記号と二つの数字 \(k, p\) を使って「\(W^{k,p}\)」と表記します。
この記号の意味は、『関数それ自体と \(k\) 階までの導関数(\(k\) 階微分)の \(L^{p}\) ノルムが定義されている関数の空間』
ということになります。
「\(L^{p}\) ノルム」については、エンジニアリングの分野でも時々出てきますので、お馴染みの方もいらっしゃるかもしれません。
\(L^{p}\) ノルムは \(p\) 乗して全部足したもののことですが、
ソボレフ空間の場合は相手が関数ですので「\(p\) 乗して全領域で積分したもの」と言った方が正確です。
\(L^{p}\) ノルムが「定義されている」という言葉には、ちゃんと計算できて「無限大にならない」というニュアンスが含まれています。
実は \(p = 2\) の場合は自動的に内積も定義されるため、ヒルベルト空間にもなります。 そこで特別に \(H\) という記号を使って「\(H^{k}\)」と書きます。 つまり、\(H^{1}\) は \(W^{1,2}\) と同じ意味になります。 以上をまとめると「\(H^{1}\)」は、関数自身の \(L^{2}\) ノルム(つまり2乗して積分したもの)と関数の1階微分の \(L^{2}\) ノルムがそれぞれ無限大にならないような関数の空間を意味します。 あるいはヒルベルト空間的に説明すれば、『関数自身とその一階微分の両方を使った内積が定義される関数の空間』とも言えます。
\(H^{1}\) に含まれる関数は、ほとんど至るところで1階微分な連続関数です。
\(H^{1}\) に含まれる関数を具体的に考えてみましょう。
まず、関数自体が無限大になると積分が計算できませんから、そのような関数は \(H^{1}\) に含まれません。
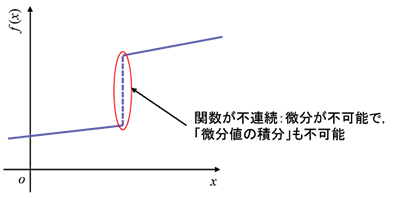
また、不連続な関数は微分が全く計算できない(強いて言えば微分が無限大になる)ので、
不連続な関数も \(H^{1}\) には含まれません。
ただ、一階微分が必ず計算できなければならないかというと、そういう訳ではありません。
一階微分の「積分ができる」という所がポイントで、積分領域をうまく分けることで計算ができるのであれば、
微分が出来ない点が多少あっても構わないのです。
「ほとんど至るところで」というと物凄く曖昧な言い方に聞こえますが、実はこれも数学の用語で、
そのような積分に影響の無い部分は無視する、というニュアンスがあります。
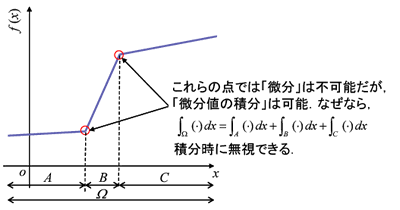
結果として、\(C^{0}\) と言って思い浮かぶような関数が \(H^{1}\) に含まれることになるのです。
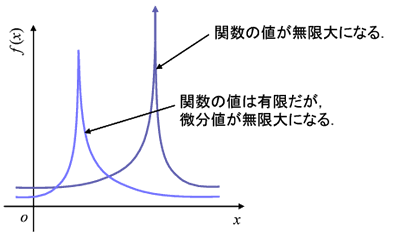
実は、\(C^{0}\) の関数の中には嫌らしい関数も含まれています。
例えば、連続だけれども値が無限大になったり、微分が無限大になるような関数も \(C^{0}\) に含まれるのですが、\(H^{1}\) には含まれません。
\(H^{1}\) という空間はまさにそのような嫌らしい関数を排除して本質的に重要な関数だけを集めたものになっているのです。
逆に言えば、\(C^{0}\) の関数の集合はそのような嫌らしい関数が含まれているために、内積やノルムの計算ができないかもしれないので「空間」とは呼ばれないのです。
*****
今回は \(H^{1}\) という関数空間について、いくつかの視点で大雑把に解説しました。
ある程度のイメージは掴んで頂けたのではないでしょうか。
次回以降、何回かに分けて \(H^{1}\) という関数空間とそれに関連する概念をさらに詳しく解説していきます。
★ご意見・ご感想はこちらへ★
![]() https://www.quint.co.jp/cgi-bin/qrepo-impr.cgi
https://www.quint.co.jp/cgi-bin/qrepo-impr.cgi
