第7話 H1勾配法の登場とその背景 その2「トポロジー最適化」
前回の記事では、形状最適化における \(H^{1}\) 勾配法である力法の計算手順について、その前に提案されていた成長ひずみ法も含めて解説しました。 この記事では、トポロジー最適化における \(H^{1}\) 勾配法について解説します。
第4話、第5話で述べたように、トポロジー最適化では当初、要素毎に設計変数を定義する方法が主流でした。 最初は、その設計変数を単純な勾配法で更新することが検討されたようです。 最も原始的なトポロジー最適化の手順は次のようなものです。
- 有限要素法で要素毎の感度を解析する。
- 感度に比例して各要素の設計変数を更新する。
- 1. に戻る。
この方法は特に理論的な不備はありません。 少なくとも勾配法が理論的に保証する範囲で最適解に収束します。 もちろん、チェッカーボードのような解に収束する可能性はありますが、初期の研究ではそれよりも最適解に至る繰り返し回数の多さが問題視されていたようです。 収束性を改善するために 2. の手順が次のように修正された「最適性基準法」が提案されました。
- 単純な勾配法 ⇒ 設計変数 \(+\) 比例係数 \(\times\) 感度 \(\Rightarrow\) 新しい設計変数
- 最適性基準法 ⇒ \((1 + \) 感度 \(/A)^{p} \times\) 設計変数 \(\Rightarrow\) 新しい設計変数(\(A \gt |\)感度\(|\))
この方法は、パラメータ \(p\) をある程度うまく決めれば単純な勾配法よりも収束が改善されたようで、しばらくの間はトポロジー最適化の主流になりました。
勾配法の観点でも、このような修正は問題ありません。
単純な勾配法とほぼ同様に最適解に収束することが保証できます。
その後、チェッカーボード現象の存在が認知されるに従って、フィルタリングの研究が進められました。 そのあたりの事情は第4回で既に述べました。 それと同時に、最適性基準法よりも収束性の良い設計変数の更新方法への研究も進められました。 設計変数の更新方法は総じて「オプティマイザ」と呼ばれ、様々な方法が提案されました。 当時のトポロジー最適化の研究者は、「フィルタリング」と「オプティマイザ」の二つに関心を持っていたようです。
その当時、私は弊社に入社したばかりだったのですが、ある研究者から「力法はどんなオプティマイザを使ってるの?」と訊かれて、私はどう答えたものか戸惑ったことがあります。 力法は前回の記事で述べたように、感度を表面力とみなして変位を解析する必要はあるものの、そこで得られた変位を節点座標に足すだけで、特に何か特別な更新方法は必要ありません。 むしろ、この一連の更新手順を「力法」と呼んでいるので、「力法のオプティマイザは力法です。」としか答えようがなかったのです。 その当時、力法は既に形状最適化の方法として一定の地位を得ていましたので、その研究者は「何か特別な更新方法を使っているに違いない」と思ったようです。 そのくらい、当時の研究者にとってはトポロジー最適化のオプティマイザには関心があったと言えるでしょう。
それと前後して、設計変数を節点に持たせて \(C^{0}\) 連続な関数で補間する方法が提案されました。 それまでは要素毎に設計変数を持たせていました。 つまり、ノンパラメトリック最適化で求めるべき関数を、従来の「要素内で一定値、要素間は不連続な関数」から「要素内は多項式で表現され、要素間は連続な関数」に変えた方法と言えます。 この方法はチェッカーボード現象を回避する方法として有力だと思われましたが、それでもアイランド現象を回避することができませんでした。 このあたりの事情は第5話で解説したとおりです。
\(C^{0}\) 連続な関数を使ってもアイランド現象が起きるという状況は、ちょうど形状最適化で波打ち現象が起きることと同じだと考えられました。 そこで、力法と同様のテクニックをトポロジー最適化にも適用した方法が、トポロジー最適化版の \(H^{1}\) 勾配法です。
トポロジー最適化版の \(H^{1}\) 勾配法の手順は次のようになります。
- 有限要素法で感度を解析する。(力法の感度とは定義が少し異なる。)
- 感度を平滑化するような偏微分方程式を解く。
- 2. で得られた解を節点値に足すことで、設計変数を更新する。
- 1. に戻る。
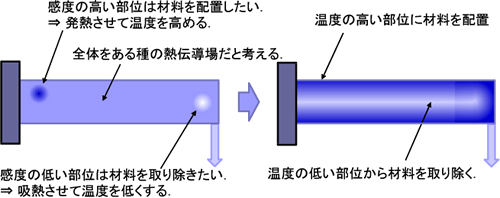
計算の手順は概ね力法と同じです。 1. の手順で計算する感度の定義は、力法の感度と少し異なりますが、力法と同様に有限要素法で計算ができます。 力法では 2. の手順で仮想的な線形静弾性解析を行うのに対して、トポロジー最適化版の \(H^{1}\) 勾配法では定常熱伝導解析に近いような偏微分方程式を解きます。 具体的に言うと、感度に比例して各部を発熱させつつ、温度に比例して各部が放熱するような熱伝導場における定常温度を求める、ということになります。 「熱伝導場」は通常の物質(金属やプラスチック)だと考えて構いません。 「感度に比例して各部を発熱」というのはジュール熱のように物体自身から熱が湧き出て来るようなイメージです。 「温度に比例して各部が放熱」というのは、熱伝達境界条件に近いのですが、物質の表面ではなく内部で起こるという点で異なります。 おそらく、これに近い物理現象は存在しないでしょう。 要するに、物理的にはやや不自然な状態を表す偏微分方程式を解いていることになります。 これはひとえに「感度の分布を近似しつつもより滑らかな関数を作るため」に使われていることになるのですが、\(H^{1}\) という関数空間を考えると非常に素直にこの偏微分方程式が導出されるのです。 このあたりの理論は、この連載の中で改めて解説します。
2. の手順はもはや「力法」というネーミングには合わなくなりました。 その当時、力法は \(H^{1}\) という関数空間における勾配法であるということが分かってきたところでしたので、形状最適化、トポロジー最適化の両方を合わせて「\(H^{1}\) 勾配法」と呼ばれるようになったのです。
*****
次回はいよいよ \(H^{1}\) 勾配法の「\(H^{1}\)」について解説していきます。
★ご意見・ご感想はこちらへ★
![]() https://www.quint.co.jp/cgi-bin/qrepo-impr.cgi
https://www.quint.co.jp/cgi-bin/qrepo-impr.cgi
