第14話 H1 勾配法とは その7「勾配法とは」
前回までの記事で、\(H^1\) 勾配法の「\(H^1\)」について解説しました。
関数空間という概念について、理解を深めていただけたでしょうか。
今回から数回に分けて、残りの「勾配法」について解説したいと思います。
はじめに、今回の記事では勾配法の概要についてお話しします。
最適化問題
勾配法についてお話しする前に、最適化問題について少し触れておきます。
最適化問題は、簡潔に言えば「目的関数と呼ばれる関数を最小にするような変数を求める問題」として数学的に定式化されます。
本来であればなんらかの制約条件を含む場合も考慮しないといけませんが、今回は簡単のため省略します。
そして構造最適化においては求めるべき変数を「設計変数」と呼ぶのでした。
設計変数が1次元の実数 \(x\) だとすると、下図のような関数 \(f\) が最小となるような \(x\) を求める問題ということになります。
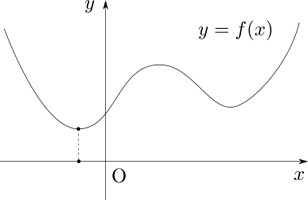
設計変数が2次元の実ベクトル \(x = (x_1, x_2)\) であれば、上図の \(x\) 軸は \(x_1 - x_2\) 平面となり、目的関数 \(f\) はその上で定義される関数として下図のように表されます。
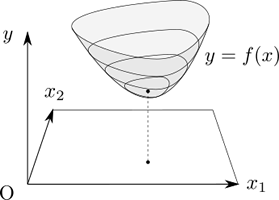
設計変数が3次元以上の実ベクトルである場合も、図示することは難しいですが、同じようなイメージとなります。
ノンパラメトリック形状最適化やトポロジー最適化のように設計変数が関数である場合も同様です。
この場合は \(f\) は関数を入力として実数を出力とするような関数、いわゆる汎関数と呼ばれるものになります。
実用的な構造最適化問題のほとんどは非線形最適化問題というものに分類されます。
ここでいう「非線形」とは「評価関数（目的関数や制約関数）が線形ではない」という意味で、たとえば先ほど図示した \(f\) のような、直線や平面のような形で表されない関数を思い浮かべていただくとよいかと思います。
勾配法
線形な最適化問題に対しては、評価関数の線形性を利用したより効率のよい解法が存在しますが、非線形最適化問題に対して最適解を直接求められる汎用的な方法は存在しません。
通常は初期解 \(x^{(0)}\) を与えてそれを
\[
x^{(k+1)} = x^{(k)} + \Delta x
\]
のように更新することを繰り返す反復法が用いられます。
この増分 \(\Delta x\) を求めるのに \(x^{(k)}\) における目的関数の勾配（傾き）\(\nabla f\left(x^{(k)}\right) = \frac{\mathrm{d}f}{\mathrm{d}x}\left(x^{(k)}\right)\) を用いる方法を勾配法と呼びます。 ざっくりと言えば、目的関数の勾配を求めて、その値が減少する方向に設計変数を動かし続ける方法ということになります。 構造最適化でよく耳にする感度とは、まさにこの勾配を表しています。
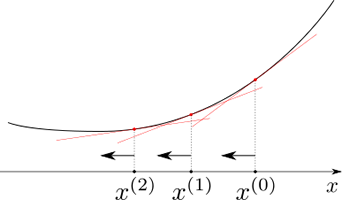
ノンパラメトリック形状最適化やトポロジー最適化など、設計変数が関数になっている場合も基本的な考え方は同じで、初期解となる関数を与えて、目的関数の勾配に基づいてそれをより良いものへと更新することを繰り返します。
ここでは設計変数を \(\phi\) という関数で表すことにしましょう。
\(\phi\) は \(x\) を与えると実数を返す関数とします。
そのような関数 \(\phi\) の初期値（初期関数）\(\phi^{(0)}\) を与えて、それを
\[
\phi^{(k+1)} = \phi^{(k)} + \Delta \phi
\]
のように更新することになります。
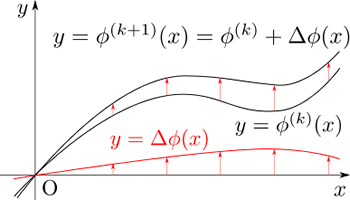
以上が勾配法の概要ですが、そのやり方ゆえに次のような特徴があります。
それは、あくまで現在の点における勾配を使って次の点への方向を決めるため、勾配法によってたどり着く解は最小点（global minimum）ではなく極小点（local minimum）となることです。
山を乗り越えた先に最小点があるような場合、通常は山を乗り越えることができず極小解に収束します。
したがって、解の初期値の選び方によっては異なる解へと収束する場合があります。
＊＊＊＊＊
今回は最適化問題の定式化を踏まえた上で、勾配法がどういう方法なのかを簡単に解説しました。
鍵となるのは、
- 目的関数の勾配が求められるか
- 勾配から設計変数の変動方向をどう決めるか
の2点です。
また、関数空間における勾配法とはまさに上述した関数の更新となるのですが、それを考えるにあたって、過去の記事で解説した種々の性質が重要となってきます。
その解説に先立ち、次回の記事では有限次元空間における勾配法について、もう少し詳しくお話ししようと思います。
★ご意見・ご感想はこちらへ★
https://www.quint.co.jp/cgi-bin/qrepo-impr.cgi
