第15話 H1 勾配法とは その8「有限次元空間における勾配法」
前回の記事では最適化問題の解法の1つである勾配法について解説しました。 今回の記事では、有限次元空間における勾配法、すなわち設計変数が有限個の実数である場合の勾配法について解説します。
*****
1次元空間における勾配法
はじめに1次元空間における勾配法を考えます。 すなわち、目的関数 \(f\) は \(f(x) = x^2 + 3x + 1\) や \(f(x) = x + \sin x\) などのような、1次元の実数 \(x\) を入力として実数を返す関数とします。 \(f\) を最小にするような解の初期値を \(x^{(0)}\) として与え、それを \(x^{(1)}\)、\(x^{(2)}\)、\(\dots\) のように更新して真の解に近づけることになります。
前回の記事では、\(f\) の勾配 \(\nabla f = \frac{\mathrm{d}f}{\mathrm{d}x}\) は \(f\) が増加するような設計変数 \(x\) の変動方向を表していることを利用して、\(f\) が減少するような設計変数 \(x\) の変動方向を求めると説明しました。
簡単に言えば1次元空間では勾配が正のときは \(x\) を減らし、負のときは \(x\) を増やせば \(f\) をより小さくできるので、
\[
a \Delta x = - \nabla f\left(x^{(k)}\right)
\]
のようにして \(x^{(k+1)} = x^{(k)} + \Delta x\) を求めるとよさそうです。
ここで \(\nabla f\) は、あくまで設計変数 \(x\) の変動方向のみを表しているので、変動の大きさを調節するための正の実定数 \(a\) をかけています。
勾配 \(\nabla f(x^{(k)})\) が得られれば、それを \(-a\) で割ることで \(\Delta x\) を求められます。
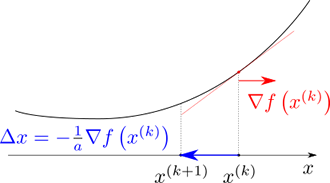
\(\Delta x\) が大きすぎても小さすぎてもよくないということは直感的にもわかるかと思います。
そのため、\(a\) の調整というのは勾配法の使用において重要なことになります。
簡単な問題であれば決め打ちでも構いませんが、汎用的に適用することを考えると自動化してしまいたいところです。
この話題については、機会があれば今後の記事で触れたいと思います。
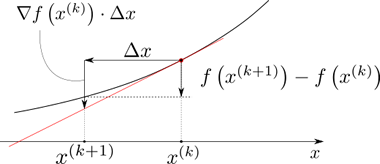
また、\(\Delta x\) が十分小さければTaylor展開を使って \[ \begin{align*} &f\left(x^{(k+1)}\right) = f\left(x^{(k)} + \Delta x\right) \\ &\simeq f\left(x^{(k)}\right) + \nabla f\left(x^{(k)}\right) \cdot \Delta x \end{align*} \] のように、すでに計算済みである \(f\left(x^{(k)}\right)\)、\(\nabla f\left(x^{(k)}\right)\)、\(\Delta x\)を用いて更新後の値を予測することができます。 \(\Delta x = -\frac{1}{a}\nabla f\left(x^{(k)}\right)\) を代入すると、\(a \gt 0\) より \[ \begin{align*} &f\left(x^{(k)}\right) + \nabla f\left(x^{(k)}\right) \cdot \Delta x \\ &= f\left(x^{(k)}\right) - \frac{1}{a}\left(\nabla f\left(x^{(k)}\right)\right)^2 \lt f\left(x^{(k)}\right) \end{align*} \] となるため、\(f\left(x^{(k+1)}\right)\) の値は \(f\left(x^{(k)}\right)\)と比べて小さくなることが言えます。
また、\(f\) の変動量 \(\nabla f\left(x^{(k)}\right) \cdot \Delta x\) のことを微分と呼んで、勾配とは区別される場合があります。 本コラムでも、勾配と言ったときは関数を設計変数で微分したもの(傾き)である \(\nabla f\) を表し、微分と言ったときは勾配と設計変数の増分の積で表される \(f\) の変動量の予測値である \(\nabla f \cdot \Delta x\) を表すことを意識しています。
簡単な例を見てみましょう。
ここでは \(f = \frac{1}{4}x^2 + x - 1\) において、\(x^{(0)} = 1\) としたとき \(f\) がより小さくなるような \(x^{(1)}\) を求めます。
まず、\(f\) の勾配は
\[
\nabla f(x) = \frac{\mathrm{d}f}{\mathrm{d}x} = \frac{1}{2}x + 1
\]
となります。
したがって、\(\nabla f\left(x^{(0)}\right) = 1.5\) となります。
この勾配を用いて \(x\) の増分を求めると、
\[
\Delta x = -\frac{1}{a} \nabla f\left(x^{(0)}\right) = -\frac{1.5}{a}
\]
となります。
あとは \(\Delta x\) が適当な大きさになるように \(a\) を決めれば、\(x^{(1)} = x^{(0)} + \Delta x\) を求めることができます。
ここでは \(a = 3\) としてみると、\(x^{(1)} = 0.5\) となります。
このとき \(f\left(x^{(1)}\right) = -0.4375\) となり、\(f\left(x^{(0)}\right) = 0.25\) より小さくなっていることがわかります。
また、このときの \(f\) の変化量は勾配と変動量の積で
\[
\nabla f(x_0) \cdot \Delta x = -0.75
\]
のように予測され、実際の \(f\) の変化量 \(f\left(x^{(1)}\right) - f\left(x^{(0)}\right) = -0.6875\) に近い値となっていることがわかります。
2次元空間における勾配法
次に2次元空間における勾配法を考えます。
ここでは設計変数を \(x = (x_1, x_2)^{\mathsf{T}}\) のように書くことにします。
ただし、\(\left(\,\cdot\,\right)^{\mathsf{T}}\) は転置を表すものとします。
このとき \(f\) の勾配は
\[
\nabla f = \left(\dfrac{\partial f}{\partial x_1}, \dfrac{\partial f}{\partial x_2}\right)^{\mathsf{T}}
\]
のようになります。
1次元のときと同様に \(f\) が増加するような設計変数の変動方向を表すのですが、ひとつ異なるのは \(f\) が「最も」増加する方向を表しているという点です。
2次元の場合も下図のように、\(-\nabla f\) 自体はひとつに決まります。
しかしこれは \(f\) が最も減少する方向というだけであり、\(\Delta x\) の向きを \(-\nabla f\) から少しぐらい変えても \(f\) は減少するということです。

一般には、2行2列の行列 \(A\) を用いて \[ A \Delta x = - \nabla f(x_{k}) \] のように表すことができます。 この行列 \(A\) は1次元空間のときの実数パラメータ \(a\) に相当するもので、実対称かつ正定値であり、\(\Delta x\) が十分小さくなるように選べば1次元空間のときと同様に \(f\left(x^{(k+1)}\right) \lt f\left(x^{(k)}\right)\) となることを示すことができます。
\(A\) が単位行列の場合は \(-\nabla f\) の方向をそのまま使うことになるので、\(\Delta x\) は現在の点 \(x_k\) において \(f\) が最も減少するような方向を表します。 この場合は特に最急降下法と呼ばれます。 一番大きく減る方向へ動かし続ければ最も早く最適解を得られるように思いますが、実際は一般に収束が遅くなることが知られています。
ここでも簡単な例を通して2次元空間における勾配法の概念を確認してみましょう。
関数 \(f(x) = x_1^2 + x_2^2\) について、\(x^{(0)} = (3, 2)^{\mathsf{T}}\) を初期解として \(f\) を減少させるような \(x^{(1)}\) を求めます。まず \(f\) の勾配は、
\[
\nabla f(x)
= \left(\frac{\partial f}{\partial x_1}, \frac{\partial f}{\partial x_2}\right)^{\mathsf{T}}
= \left(2x_1, 2x_2\right)^{\mathsf{T}}
\]
となります。
したがって、\(\nabla f\left(x^{(0)}\right) = (6, 4)^{\mathsf{T}}\) となります。
今回は \(A\) を単位行列を10倍したものとすると、\(x\) の増分は
\[
\Delta x = -\frac{1}{10}\nabla f\left(x^{(0)}\right) = (-0.6, -0.4)^{\mathsf{T}}
\]
となり、\(x^{(1)} = (2.4, 1.6)^{\mathsf{T}}\) が得られます。
このときの目的関数の値は \(f\left(x^{(1)}\right) = 8.32\) となり、\(f\left(x^{(0)}\right) = 13\) より \(4.68\) 小さくなっていることがわかります。
このときの \(f\) の変化量も、勾配と増分の積(内積)を用いて
\[
\nabla f\left(x^{(0)}\right) \cdot \Delta x
= -\frac{26}{5} = -5.2
\]
のように予測することができます。
ちなみに、3次元以上の空間についても2次元空間の場合と同じように話を進めることができます。
設計変数が \(d\) 次元ベクトルのとき、目的関数の勾配も同じ \(d\) 次元ベクトルになります。
その勾配を少し加工して設計変数に足すことを繰り返すという流れが、これまでの話で理解いただけたでしょうか。
*****
今回の記事では1次元および2次元の空間の場合に焦点を当てて、有限次元空間における勾配法の具体的な手続きを見てきました。 これを基にして、次回の記事では関数空間、特にHilbert空間における勾配法について解説します。
★ご意見・ご感想はこちらへ★
![]() https://www.quint.co.jp/cgi-bin/qrepo-impr.cgi
https://www.quint.co.jp/cgi-bin/qrepo-impr.cgi
