第16話 H1 勾配法とは その9「関数空間における勾配法」
前回は有限次元空間における勾配法の手続きを、1次元空間の場合と2次元空間の場合で確認しました。 今回の記事では関数空間における勾配法について解説します。
*****
関数空間における勾配法は、有限次元空間における勾配法の概念を拡張したようなものとなります。 有限次元空間のときは、\(d\) 次元実ベクトルで表される設計変数 \(x\) の初期値 \(x^{(0)}\) を決めた上で、以下の手順により設計変数の更新を繰り返していました:
- 目的関数の勾配 \(g\) を求める。
- 勾配に基づいて設計変数の変動方向を求める(\(g \to \Delta x\))。
- 設計変数を更新する(\(x^{(k+1)} = x^{(k)} + \Delta x\))。
関数空間のときも同様に、関数で表される設計変数 \(\phi\) の初期値(初期関数)\(\phi^{(0)}\) を決めた上で、同じ手順により設計変数の更新を繰り返して \(\phi^{(1)}, \phi^{(2)}, \dots\) を求めていきます。 ただし、形状最適化やトポロジー最適化においては設計変数である関数が \(H^1\) 級であることを初めに想定します。 \(H^1\) 級である限りは形状最適化における波打ち現象やトポロジー最適化におけるアイランド現象を表すような奇妙な関数をそもそも表現できないので、 この想定が維持されているかぎりは滑らかな形状・密度分布が得られることになります。
以下では、上記の手続きでこれまでの有限次元空間の場合と異なる部分について解説します。
1.目的関数の勾配を求める
はじめに、有限次元空間のときと同様に目的関数の勾配を求める必要があります。 前回の記事では、有限次元空間における勾配は通常の微分もしくは偏微分を用いて求められることをお話ししました。 関数空間における勾配を求めるためには、より一般化した微分の定義を用いる必要があります。 今回の記事では詳細まで立ち入りませんが、これにより目的関数の勾配 \(g\) を得ることができます。 OPTISHAPE-TS をお使いいただいたことのある方はよくご存知かと思いますが、TS Studio で表示することができる感度のコンター図はこの勾配を可視化したものと言えます。
有限次元空間における勾配は設計変数と同じ \(d\) 次元実ベクトルとなっていました。 言い方を変えれば、勾配が属する線形空間は設計変数が属する線形空間と同じ、\(d\) 次元実ベクトル全体の集合 \(\mathbb{R}^d\) であるということになります。 そのため \(\Delta x\) として \(-g\) をそのまま使ったとしても更新された設計変数はもちろん \(d\) 次元ベクトルなので、なんの問題もありません。
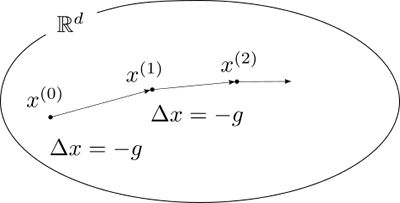
一方で、関数空間における勾配が属する線形空間はある関数空間となります。 しかし有限次元空間のときとは異なり、この関数空間は設計変数が属する関数空間とは一般には一致しません。 つまり、\(\phi^{(k+1)} = \phi^{(k)} + \Delta\phi\) で設計変数を更新する際に \(\Delta\phi\) として \(-g\) をそのまま使うと、 \(\phi^{(k+1)}\) の属する関数空間が変わってしまい、滑らかさが失われてしまう場合があります。 そのことが形状最適化・トポロジー最適化で数値不安定現象が生じる一因になっていると考えられています。
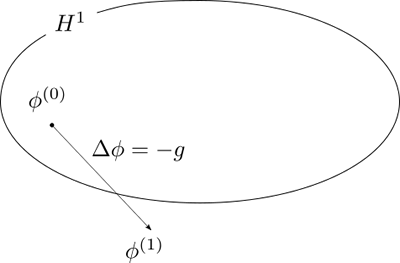
そこで、次の手順によって設計変数の変動方向 \(\Delta \phi\) が元の関数空間に属するような、言い換えれば設計変数の滑らかさを回復させるような処理が必要となるわけです。
2. 勾配に基づいて設計変数の変動方向を求める
有限次元空間では、連立1次方程式 \(A\Delta x = -\nabla f\) の解として設計変数の増分 \(\Delta x\) を求めていました。 関数空間でこれに相当するのが偏微分方程式の境界値問題となります。 その概要については第6話や第7話の記事で触れたとおりです。
しかし偏微分方程式であればなんでもよいというわけではなく、弱形式で表現したときの \(H^1\) 上の双1次形式が強圧かつ有界であるものを選ぶ必要があります。 聞きなれない言葉が並んでいるかもしれませんが、「\(H^1\) 上の双1次形式」は2つの \(H^1\) 級の関数を引数に取ってなんらかの値を返すような関数(汎関数)のことで、連立方程式における係数行列に相当するものとなります。 また、「強圧」はその係数行列が正定値であることに、「有界」は係数行列のノルムが有界であることに相当する性質を表します。 こうした条件を満たす偏微分方程式の解は \(H^1\) 級となるため、設計変数の増分 \(\Delta\phi\) を \(H^1\) に戻すことができます。
たとえば \(H^1\) における内積が \[ (f, g)_{H^1} = \int_{\Omega} f(x) g(x) \,\mathrm{d}x + \int_{\Omega} \dfrac{\mathrm{d}f(x)}{\mathrm{d}x} \dfrac{\mathrm{d}g(x)}{\mathrm{d}x} \,\mathrm{d}x \] で表されることは第12話の記事でお話ししましたが、これは \(H^1\) 上の強圧的かつ有界な双1次形式の1つの例となります。 また、2つの被積分関数に正の定数 \(c_1\)、\(c_2\) をそれぞれかけて \[ (f, g)_{H^1}^{\prime} = \int_{\Omega} c_1 f(x) g(x) \,\mathrm{d}x + \int_{\Omega} c_2 \dfrac{\mathrm{d}f(x)}{\mathrm{d}x} \dfrac{\mathrm{d}g(x)}{\mathrm{d}x} \,\mathrm{d}x \] としてもかまいません。 第2項は平滑化に関する項となるのですが、\(c_1\) と \(c_2\) を用いてその度合いを調節することができるのです。 トポロジー最適化ではこの式を用いて表される偏微分方程式を解いて設計変数の変動方向を求めています。
ちなみに、定常熱伝導問題における双1次形式は熱伝導率を \(\lambda\) とすると \[ a(f, g) = \int_{\Omega} \dfrac{\mathrm{d}f(x)}{\mathrm{d}x} \cdot \left( \lambda \dfrac{\mathrm{d}g(x)}{\mathrm{d}x} \right) \,\mathrm{d}x \] のように表されます。 \((f, g)_{H^1}^{\prime}\) と比べると違いは \((f, g)_{H^1}^{\prime}\) の第1項の有無ぐらいで、似たような形をしていることがわかります。 第12話で「トポロジー最適化版の \(H^1\) 勾配法では定常熱伝導解析に近いような偏微分方程式を解きます」とお話ししたのはこのためで、定常熱伝導解析における双1次形式が \(H^1\) における内積に近い形をしていることに起因しています。
形状最適化では線形弾性問題における双1次形式(いわゆる剛性行列に相当するもの)をそのまま用いたものが力法と呼ばれています。 この双1次形式は強圧性を備えていませんが、拘束条件(Dirichlet境界条件)を課すことで強圧性を持たせています。 また、この双1次形式を応用したものとしてばねつき力法と呼ばれるものも存在します。 これはイメージとしてはモデルの境界上に分布ばねを配置するようなもので、拘束条件がなくても、つまり形状の変動を拘束する部分が存在しなくても強圧性があるものとなります。
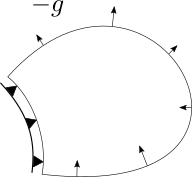
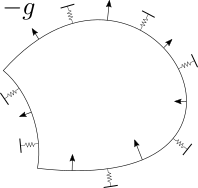
このように、勾配から設計変数の変動を求めるときには様々な偏微分方程式を選ぶことができます。 そしてそのすべてを総称したものが \(H^1\) 勾配法と呼ばれているのです。 ときおり「力法と \(H^1\) 勾配法はどう違うのか」という質問をいただくことがありますが、「力法は \(H^1\) 勾配法の1つの例である」、 あるいは「\(H^1\) 勾配法は力法を一般化したものである」ということがおわかりいただけたでしょうか。
3. 設計変数を更新する
\(\Delta\phi\) を求めることができればそれを \(\phi^{(k)}\) に足すだけなので、更新そのものは有限次元空間のときとまったく同じです。 しかし、第11話の記事で紹介した完備という性質がここでも重要となります。 つまり、更新を繰り返して得られる関数列 \(\left\{ \phi^{(0)}, \phi^{(1)}, \phi^{(2)}, \dots \right\} \) の個々の要素が \(H^1\) 級であっても、 それが収束する関数 \(\lim_{k \to \infty} \phi^{(k)}\) が \(H^1\) に属することが保証されていなければなりません。 完備という性質はそれを保証するものなので、安心して設計変数の更新を繰り返すことができるのです。
*****
今回は関数空間における勾配法について解説しました。
長きにわたって続いた \(H^1\) 勾配法の解説はこれで一区切りとなります。
厳密な議論や数式をなるべく避けて記述したので(避けられなかった部分もありましたが・・・)、腑に落ちない点など多々あったかと思います。
次回からは、OPTISHAPE-TSのユーザーの皆様からよくある質問をはじめとして、 これまでの連載で割愛した詳細な部分などで参考になるであろう話題を取り上げる予定です。ぜひ引き続きご覧いただければと思います。
★ご意見・ご感想はこちらへ★
![]() https://www.quint.co.jp/cgi-bin/qrepo-impr.cgi
https://www.quint.co.jp/cgi-bin/qrepo-impr.cgi
