第7話 大学の研究成果を商用ソフトウェアへ
1982年に、Ann Arborにあるミシガン大学に菊池昇准教授(現 名誉教授)を訪ねました。 有限要素法の話題で3時間ほど話をしたのですが、とても興味深かったのは、「有限要素法の品質管理が出来るかも知れない」という言葉でした。
この話が忘れられず1984年に再度菊池先生をミシガン大学に訪ね、「あの時に伺った有限要素法の品質管理はその後進展しましたか?」と尋ねると、
当時博士課程の学生だった鳥垣さん(現 日産自動車)が、中心部に亀裂がある四角い平板の両端を引っ張った時の亀裂先端の応力が、元のメッシュ形状に較べ、
メッシュのトポロジーを一切変えずに3倍になったというグラフを見せてくれました。
下図の板は弾性体を仮定しているので、亀裂先端部の応力は弾性論では無限大になりますが、限られた数の要素分割でも、節点の座標位置を変える(r法)だけでこれ程の違いが出ることに驚きを覚えました。
誤差解析を基に、評価した誤差測度に従って、節点の座標を移動させ、近傍の相対誤差を最小化する方法だとの説明を受けました。
他に、同じ問題で、評価した誤差測度の大きな要素をさらに細分割する方法(h法)も見せていただきました。
これは物理量の変化が急なところをどんどん細かくするので、当然精度は上がるのですが、計算時間も一緒に大きく増えるので、私は前者のr法に深い感銘を受けました。
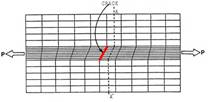
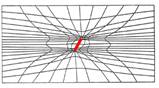

An example of stress analysis using adaptive finite element method
Initial FE mesh(Left), Adaptive refinement mesh by using r-method(Center),Mises stress(Right)
そこで、このプログラムを日本で商品化したいと菊池先生に直接打診したところ、ご快諾をいただきスタートしました。大学とのコラボ製品第1号、アダプティブ有限要素法ソフトウェア OPTIMESH です。
前述のくいんとセミナーの効果もあって、第一弾としてはほぼ成功だったと思います。
そして、この誤差解析を基にしたメッシュ改良法に携わったことが、逆に有限要素そのものの精度に興味を持つことになりました。 顧客からもMSC/NASTRANの各要素の信じられない高精度の話を聞き、昔SAP4で経験したWilsonの非適合要素を思い出しました。
それから、文献を色々調べ、Pian-Sumiharaの要素、Fujino-Moreleyの要素、・・・と調べて行くと、菊地文雄先生の研究にたどり着きました。 そこで、第一人者である菊地文雄教授を東京大学数理科学研究科に訪ね、ご指導をお願いすると、幸運にもご快諾いただき、一緒に要素開発に参加させていただくことになりました。
その後、述べ20年に渡り菊地先生にご指導いただいて開発した要素は、低次の形状関数を用いていても、曲げ、剪断にも良い応答を示し、これまでよりもロッキングを回避しやすい要素が出来上がりました。
Computational Mechanicsに載った論文を見たとのことで、九州在住の住原さん(Pian-Sumihara要素の当事者)から電話と丁寧な手紙をいただいたりしました。
余談ですが、「大学の素晴らしい研究成果をソフトウェアとして商用化し、製造業の役に立つ」という我々のビジネスモデルは、 90年代半ばに文部科学省が全国の国立大学、メジャーな私立大学にTLO(Technology Licensing Organization)を作る10年前の事です。
*****
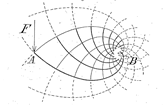
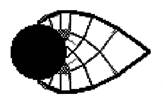
さて、次のテーマを探し始めた頃、ミシガン大学で衝撃的な画像を目の当たりにしました。 当時大学院博士課程の学生であった鈴木克幸さん(現 東京大学教授)が見せてくれたミッチェルの文献にあるトラスをトポロジー最適化で再現した画像です。 オリジナルのミッチェルの論文は1904年に出版されていますが、その中に出ている 「離れた2点の片方に垂直な力を、もう片方には釣り合うモーメントを負荷した時の最小構成の梁は、直交した螺旋状の形」(下図左)というものです。
Michell AGM.
The Limits of Economy of Material in Frame Structures,
Philosophical Magazine Series 6, 8, pp.589-597.
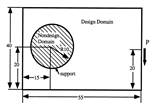
真ん中の図に示す、長方形板の左側を大きな円盤で固定し右端に鉛直荷重を負荷した時に、領域の材料を20%に制約した時の、最も剛性の高い構造形態を連続体要素で作ったのがこれ(下図右)だというのです。
その時、直感しました。
「今までの数値シミュレーションは、決まった形状、材質において、外的境界条件の下にその構造の挙動を模擬するものだったけれど、この絵は逆だ。
ということは、使う人に構造の基本となる高剛性を持つ形態、つまり本質をついたアイディアを提案できることになる。これは凄いぞ!」
ここで、2年前に菊池先生がデンマークから、オフィスに電話を下さったことを思い出しました。 興奮した声で、「石井さん、今サバーティカルでデンマーク工科大学にいるけど、面白い最適化をMartinと一緒に考えた。 ミシガンに戻ったら見せるから来てよ。」
「そうか、これがあの時の最適化が発展したものか。これはいけるぞ。」
その後、克幸さんの作ったプログラムをいただき、自分で隅から隅まで読み、少しずつ商用に耐えるよう改修を続けました。
Bendsoe, M. P. and Kikuchi, N.
Generating optimal topologies in structural design using a homogenization method,
Computer Methods in Applied Mechanics and Engineering 71 (1988), pp.197-224.
Suzuki, K. and Kikuchi, N.
Shape and topology optimization using the homogenization method,
Computer Methods in Applied Mechanics and Engineering 93 (1991), pp.291-318.
こうして、プログラムを整理し改修しながら、多くのテストを繰り返し、 トポロジー最適化プログラムOPTISHAPE として、1989年10月に正式に商用ソフトウェアとしてリリースしました。
*****
次回は、この OPTISHAPE が採用した設計領域を多孔質体と仮定したときの計算法:均質化法のお話と、リリース後の様子も書きたいと思います。
第8話に続く...
自宅にて.
石井 惠三
★ご意見・ご感想はこちらへ★
 https://www.quint.co.jp/cgi-bin/qrepo-impr.cgi
https://www.quint.co.jp/cgi-bin/qrepo-impr.cgi
