第29話 シグモイド関数
今回は、ある決められた範囲の値を取る関数の最適化問題を考えるときのアイデアに関するもので、シグモイド関数(sigmoid function)についてお話しします。
*****
\(H^1\) 勾配法を用いてノンパラメトリック最適化問題を解く際は、設計変数となる関数の初期値が与えられていて、それに増分となる関数を足すことで設計変数を更新することを考えるので、この関数は線形空間の要素でなければなりません。 線形空間については第9話で解説しましたが、かなり前の記事になるので復習も兼ねて丁寧に説明してみます。
たとえばトポロジー最適化の密度を表す関数を考えてみましょう。 ここではそれを \(\phi\) と表記することにします。 \(\phi\) は最適化問題を考える連続体 \(\Omega\) を定義域とし、\(\require{physics} \qty[0, 1]\) を値域とする関数となります。 このような関数は無数に考えることができるので、それらをすべて寄せ集めたものを集合 \(X\) と表すことにしましょう。 最適化問題を解くということは、集合 \(X\) の中から解となる関数を見つけるということに相当するのでした。
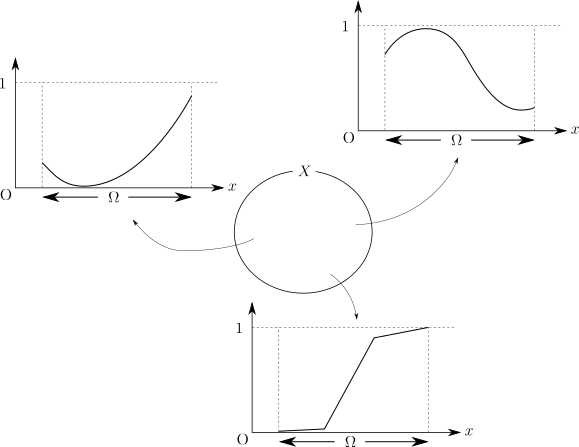
さて、集合の中でも、それに属する元同士になんらかの関係性が定まっているものを空間と呼ぶのでした。 線形空間はそのような空間の中でも最も基本的なもののひとつとして位置づけられるもので、「ある集合が線形空間である」ためには、その集合に属する元同士の和が定義されていたり、スカラー倍が定義されていたり、といったいくつかの条件を満たしている必要があるのでした。 集合 \(X\) の場合を考えると、その要素である関数を適当に2つ選ぶと和は定義できますし、実数 \(c\) を1つ選べばスカラー倍された関数を考えることもできるので、この点に関しては問題ありません。
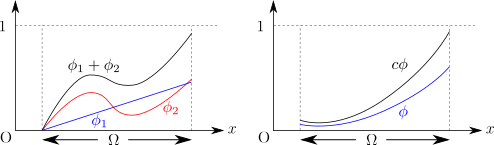
しかし線形空間であるためには、このような和やスカラー倍の結果として得られた関数がもとの集合 \(X\) の元となる必要もあります(このことを和やスカラー倍について閉じているともいいます)。 今回の場合、値域が \(\qty[0, 1]\) の関数を2つ選んで足し合わせた関数の値域は \(\qty[0, 2]\) となってしまいますし、実数 \(c\) 倍した関数の値域は \(\qty[0, c]\) となるので、\(X\) の要素にはなりません。 したがって \(X\) は線形空間にならず、数学的には勾配法で最適解を求める際の土俵に立つことすらできないのです。

*****
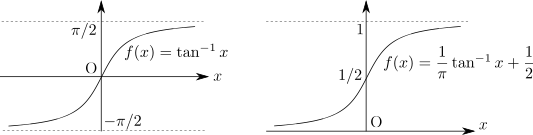
そこで考えられたのが、シグモイド関数と呼ばれる別の関数を媒介して問題を構成する方法です。 ローマ字の S がギリシャ文字のシグマ(\(\sigma, \Sigma, \varsigma\))に相当するのですが、その名の通り S の形をした関数をまとめてこのように呼びます。 たとえばひとつの例に逆正接関数 \[ f\qty(x) = \tan^{-1} x \] があります。 この関数は実数全体を定義域として \(\qty(-\pi/2, \pi/2)\) を値域に持ちます。 今回は値域を \(\qty(0, 1)\) にしたいので、\(1/\pi\) 倍して \(1/2\) を加えた \[ f\qty(x) = \dfrac{1}{\pi} \tan^{-1} x + \dfrac{1}{2} \] を使います。
*****
この関数を使って、設計変数が属する空間が線形空間となるようにすることを考えてみましょう。 まず、設計変数として新たな関数 \(\theta\) を用意します。 これは領域 \(\Omega\) を定義域として、実数全体を値域とする関数とします。 値域が実数全体であれば、関数同士の和やスカラー倍について閉じるようになり、線形空間として要請される条件を満たします。 そこでこのような関数全体の集合は線形空間となり、数学的にも最適化の対象とすることができるようになります。
続いて、設計変数 \(\theta\) からシグモイド関数 \(\phi\) を介して得られる値を、本来は設計変数として考えたい値として使います。 この関数は \(\theta = 0\) のときに \(\phi = 1/2\) となり、\(\theta \to \infty\) で \(\phi \to 1\)、\(\theta \to -\infty\) で \(\phi \to 0\) となります。 たとえば密度法によるトポロジー最適化で線形弾性問題を考える場合であれば、Young率に \(\phi\) をかけることになります。 SIMPモデル(Solid Isotropic Material with Penalization)を採用するのであれば、シグモイド関数 \(\phi\) のべき乗を乗じます。
また、設計変数に対する評価関数の微分を求めるときは、代わりにシグモイド関数の微分を求めることになります。 たとえば上記の逆正接関数の場合は \[ f^\prime\qty(\theta) = \dfrac{1}{\pi}\dfrac{1}{1 + \theta^2} \] となり、これが本来は設計変数の微分が必要なところで現れることになります。 意味するところとしてはまさに上述したシグモイド関数のグラフの傾きで、\(\theta = 0\) で最大となり、\(\theta \to -\infty\) または \(\theta \to \infty\) でゼロへと収束していきます。
*****
値そのものを直接設計変数にするのではなくこのような関数を介することで、領域上である決められた範囲の値を取る関数の最適化問題を考えることができるようになります。 ちなみに、OPTISHAPE-TSでご利用いただけるビード最適化でも、同じ原理を応用して板構造の法線方向に対するオフセット量の分布を最適化しています。
★ご意見・ご感想はこちらへ★
![]() https://www.quint.co.jp/cgi-bin/qrepo-impr.cgi
https://www.quint.co.jp/cgi-bin/qrepo-impr.cgi
