第2話 ノンパラメトリック最適化の難しさ その1「関数の最適化」
前回の記事では、ノンパラメトリック最適化について簡単に説明しました。 その中で、ノンパラメトリック最適化は関数を最適化する方法だと述べました。 この記事では、「関数を最適化する」とはどういうことか、イメージを深めて頂くために、それがどのような難しさを持っているのかという視点で解説します。
＊＊＊＊＊
既に述べたように、パラメトリック最適化はそれぞれ独立したいくつかの設計変数を最適化します。 通常は、設計変数の数は数個～数十個以内でしょう。 もしかしたら数百個、数千個かもしれませんが、無限個にはなりません。 当たり前ですが。数学的に言えば、有限次元空間上の一点を求める問題を解いていることになります。 一方、ノンパラメトリック最適化の「関数を最適化する」という事を、より数学的に表現すると、関数空間上の一つの関数を求める問題を解くこと、と言うことができます。 「関数空間」という言葉が分かりにくいと思いますが、ひとまず「あり得る関数を全部集めたもの」という程度に理解しておくと良いでしょう。
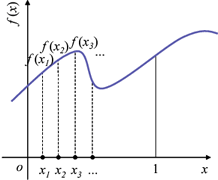
「一つの関数を求める」とはどういうことか、簡単な関数 \(f\) を例に考えてみましょう。
変数 \(x\) は \(0\) ～ \(1\) の間の値（実数）をとることにします。
\(f\) が関数である、ということは変数 \(x\) の値を一つ決めると、それに応じて \(f(x)\) の値が一つ決まる、ということです。
変数 \(x\) は \(0\) ～ \(1\) の間で無限個ありますから、その無限個それぞれについて \(f(x)\) が決まる、ということなのです。
つまり、「一つの関数を求める」ということは、「無限個の値を決める」ということになるのです。
これは次のようにも説明できます。
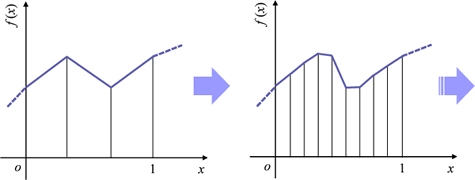
関数を近似する方法はいろいろあります。
例えば、多項式近似、フーリエ変換、テーラー展開、有限要素近似等々です。
いずれの近似方法でも、任意の関数を正確に表現するためには無限に多くの項を計算する必要があります。
つまり、どのような表現方法を使っても関数を一つ求めるためには無限個の値を全て決める必要があるのです。
従って、ノンパラメトリック最適化は無限個の数値を求める問題、あるいはもっと数学的に言えば、無限次元空間上の一点を求める問題を解いているとも言えるのです。 先に「関数空間」という言葉が出てきましたが、関数空間の次元は無限大です。 「関数空間」とか「無限次元空間」というと、なにか突拍子もないもののように思えるかもしれませんが、\(H^{1}\) 勾配法を理解する上では重要な概念になります。 「関数空間、無限次元空間とは何か？」という疑問はさておき、ノンパラメトリック最適化は無限個の数値を求める問題を解いているという点で、パラメトリック最適化よりも難しそうだ、ということは理解して頂けたのではないでしょうか？
ここで種明かしをしますが、実際にはもちろん無限個の数値を計算する訳ではありません。 ノンパラメトリック最適化では、求めるべき関数は有限要素法等の手法で離散化されて、有限個のパラメータで近似されますので、結局は有限個の数値を求める問題に帰着します。 従って、有限個か無限個かという区別はこの時点で無くなってしまいます。 それでも、求めるべき設計変数の数は有限要素モデルの規模（節点数、要素数）と同程度になりますから、非常に大きな数になります。 現在は数十万～数百万節点のモデルが一般的に解析されていますから、ノンパラメトリック最適化は実質的に数十万～数百万次元空間の中から１点を求める問題になります。 この次元の大きさがノンパラメトリック最適化の難しさになります。 次元が非常に大きくなるため、上手い最適化アルゴリズムを使わない限り、現実的な計算時間で最適解を求められないのです。
＊＊＊＊＊
次回は最適化アルゴリズムの観点でさらに解説していきます。
★ご意見・ご感想はこちらへ★
https://www.quint.co.jp/cgi-bin/qrepo-impr.cgi
