概要に戻る2．VOXELCONを活用した簡易モデルの材料パラメーター算出
解析モデル
モデルコリレーションを行う解析モデルは、六面体要素の簡単なメッシュで構成されます。
本事例の場合、実物のパネル内のコア材はハニカム構造ですが、 VOXELCONの均質化解析機能 を使用することで、 中身の詰まった簡易モデルで、ハニカム構造に等価な材料パラメーターを算出します。 （実物を再現するような細かいハニカム構造のモデルを作成する必要はありません。）
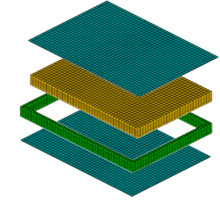
均質化解析：簡易材料パラメータ算出
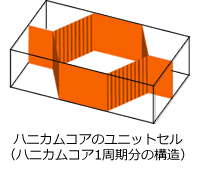ハニカムコアのユニットセルに対し、VOXELCONの均質化解析を用いて等価な物性値を求めます。
周期性をもつ構造全体の1周期分を取り出したセルのこと。
ユニットセルに対して均質化解析を用いることで、物性値を求めることができます。
右図の例では、直方体部分がユニットセルに相当します。
◎ 直交異方性材料 ◎
応力 {σ} とひずみ {ε} を関連付ける構成式の弾性コンプライアンスマトリクス [D]-1
の直交異方性材料の9つのパラメータを求めます。
各パラメータ詳細
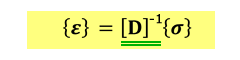
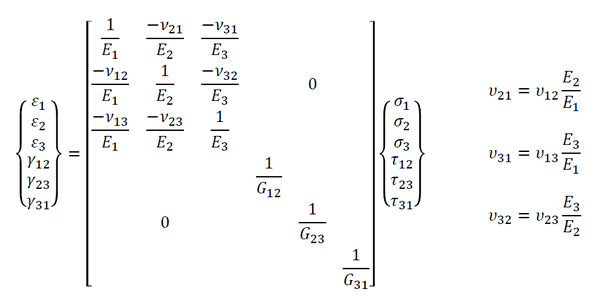
解析結果
| ヤング率 | E1 = 0.56085E+00 | E2 = 0.56045E+00 | E3 = 0.70398E+03 |
|---|---|---|---|
| ポアソン比 | V12 = 0.99853E+00 | V23 = 0.15100E-03 | V31 = 0.49052E+00 |
| せん断弾性率 | G12 = 0.38111E-01 | G23 = 0.96322E+02 | G31 = 0.14409E+03 |
解析結果のモード形状
均質化解析では、本来複雑になりうる「構造」を、その構造より大きいスケール（マクロスケール）の観点での「材料」ととらえます。
このことにより、途方もなく複雑な構造であっても、シミュレーション上では単純に中身の詰まったメッシュを作成し、均質化解析で得られた材料を割り当てることで、
その複雑な構造と等価な構造を再現することができます。
また、均質化解析で得られるのは材料パラメーターのため、異方性材料に対応しているどのようなソフトウェアでも連携が可能です。
NX Nastran による固有振動解析
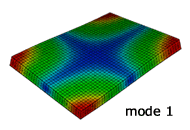
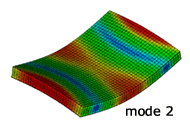
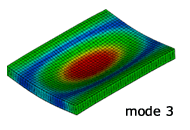
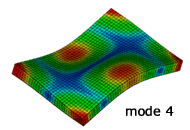
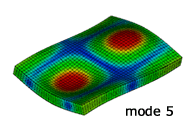
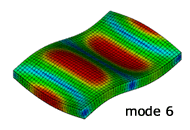
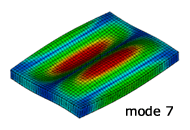
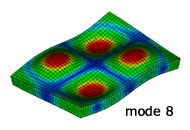
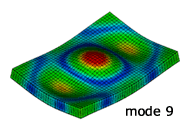
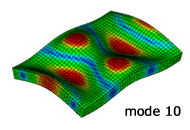
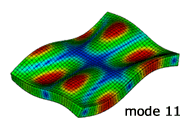
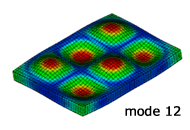
実験との比較
◎ 固有振動数の比較 ◎
| モード | FEM/実験 |
|---|---|
| 1 | 101.44% |
| 2 | 104.41% |
| 3 | 86.058% |
| 4 | 95.699% |
| 5 | 100.15% |
| 6 | 99.088% |
| 7 | 92.678% |
| 8 | 95.740% |
| 9 | 98.427% |
| 10 | 101.21% |
| 11 | 102.30% |
| 12 | 99.824% |
| 13 | 102.21% |
| 14 | 102.06% |
| 15 | 106.26% |
| 16 | 113.79% |
実験結果とVOXELCONで求めた材料パラメーターを適用した固有振動数の比較は左の表のとおりです。
このほか、MAC※ を用いて比較をしておりますが、詳細は割愛いたします。
※ MAC（Modal Assurance Criterion）
VOXELCONでの均質化解析では、実験の値を全く参考にせずに解析をおこないました。 実験とシミュレーションの相違が許容範囲かどうかは適用者次第ではありますが、 ここから最適化をおこなって誤差を縮めていく場合にも、良好な初期解となることは確実です。
この後は、この誤差を小さくするために下記2種の最適化ソフトウェアを活用し、
それぞれに精度の高いモデルコリレーションへ導きます。
AMDESSを活用した材料パラメータの同定
OPTISHAPE-TSを活用したモデル形状変更による同定
ではまず、『3A．AMDESSを活用した材料パラメータの同定』からご説明します。
 |
 |
