第5話 ノンパラメトリック最適化の難しさ その4「波打ち現象」
前回はトポロジー最適化の難しい問題としてチェッカーボード現象があることを説明しました。 また、その回避策としてフィルタリングというテクニックがあるのですが、そのさじ加減が難しいことを解説しました。
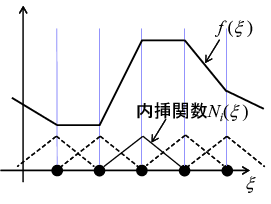
フィルタリングとは全く違うアプローチで、最適化問題に修正を加えずに、チェッカーボードを回避するための方法も提案されました。 設計変数を要素毎ではなく節点毎に持たせて、要素内を \(C^{0}\) 連続な関数で補間する、というアイデアです。
\(C^{0}\) 連続を仮定すると、そもそもチェッカボードのような関数が表現できませんので、この方法は本質的にチェッカーボード現象は起こり得ません。 また実用上もかなり有力な方法で、多くのトポロジー最適化問題でエンジニアが満足するような最適解が得られるようになりました。

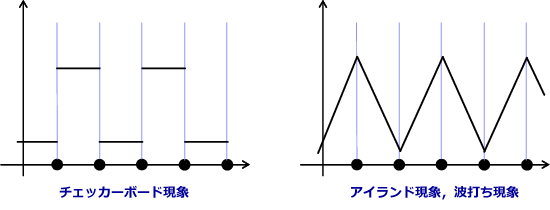
しかしながら、「アイランド現象」と呼ばれる現象が僅かながら起こり得ることが分かってきました。 この現象は、周囲の密度がゼロ(材料が配置されない)にもかかわらず離れ小島のように密度の高い部分が現れる現象です。 構造物の一部が宙に浮いている状態に見えるので、当然のことながらエンジニアの視点では「有り得ない」構造だと言わざるを得ません。 ところが、この現象もチェッカーボードと同様に解析上は「有り得る」構造で、十分な剛性を持っていて繋がった構造物として解析されているのです。 これは \(C^{0}\) 連続版のチェッカーボード現象とも言えます。 アイランド現象を避けるためには、やはりフィルタリングまたはそれに近いテクニックを併用する必要があります。

ここで、トポロジー最適化から少し離れて、形状最適化の話に移ります。 形状最適化では有限要素メッシュ自体を移動させますが、有限要素メッシュの形状はもともと \(C^{0}\) 連続な関数で表現されていますので、トポロジー最適化のチェッカーボード現象に相当するものは起こり得ません。 ところが、ここでも「波打ち現象」と呼ばれる表面が凹凸になる現象が起こることが知られていました。 これはトポロジー最適化のアイランド現象と同様な状況になっていたと言えます。

この波打ち現象を回避するために、形状最適化においてもフィルタリングのような処理は考えられますが、有限要素メッシュ自体を移動させるというアイデア自体が長い間諦められていたようです。
例えば、有限要素メッシュの節点を直接移動させる代わりに境界線をスプライン曲線で表現して、その制御点を移動させるという方法が考えられていたようです。 ただ、この方法は三次元への拡張を考えると実用は難しいと思われます。 また、有限要素メッシュの形状変化を少数の変形モード(基底ベクトル)の重ね合わせで表現し、その少数の重み係数を設計変数として最適化を行う方法(基底ベクトル法)も提案されました。 形状の変化を制限する、ということは設計変数の数を少なくすることにもなりますから、前回の記事で述べたような設計変数が多いことによる解法の難しさも避けることができます。 実際、基底ベクトル法はパラメトリック最適化の一つとして位置付けられていて、ノンパラメトリック形状最適化とは区別されます。
結局のところ、トポロジー最適化でも形状最適化でも最適化すべき関数に凹凸が現れて、滑らかさが失われてしまうということが、実はノンパラメトリック最適化に共通する難しい点なのです。 凹凸が現れないようにするには、最適化の過程で関数に何らかの平滑化を行うか、または関数の滑らかさが維持されるように制限を加えながら最適化を行う必要があります。
前述のフィルタリングは前者の代表で、形状をスプライン曲線で表現するのは後者と言えます。 トポロジー最適化で \(C^{0}\) 連続な関数を使う、というのも後者の方法と言えますが、制限が不十分なためにチェッカボードとは少し違った形で凹凸が現れたのです。 また、基底ベクトル法も後者の方法と言えますが、形状の変化が極端に制限されて、もはやノンパラメトリックではなく、パラメトリック最適化になってしまった、と考えることができます。 実は \(H^{1}\) 勾配法は、実質的に前者のような処理方法を採りながら数学的には後者のような制限を加えたものと解釈できる、という少し変わった位置付けの方法なのです。
\(H^{1}\) 勾配法では、上で述べたフィルタリングのように周囲の要素や節点で平均化する代わりに偏微分方程式を解いて滑らかさを回復させます。 近年では、トポロジー最適化の過程で偏微分方程式をフィルタリング代わりに使う方法が数多く提案され、それらを総称して「PDE フィルター」と呼ばれることがあります。 トポロジー最適化における \(H^{1}\) 勾配法は PDE フィルターの一つと言えます。 ただし、前回の記事で述べたように一般的なフィルタリングは最適化問題に何らかの修正を加えることに相当しますので、フィルタリングが本来の最適化問題に影響を与えてしまい、そのさじ加減が難しいのですが、\(H^{1}\) 勾配法では最適化問題には本質的に影響を与えません。 \(H^{1}\) 勾配法でも平滑化の効果の大小は調整できるのですが、あまり神経質にパラメータを調整しなくても概ね良好な解が得られます。
詳細は、この連載で順を追って説明する必要がありますが、「\(H^{1}\)」というのはある種の関数空間(関数の集まり)で、その \(H^{1}\) の中で勾配法を自然な形で適用すると、トポロジー最適化の PDE フィルターのような処理になるのです。 あるいは、関数を \(H^{1}\) の中に制限した勾配法が \(H^{1}\) 勾配法であるとも言えます。 ただ、「\(H^{1}\) の中に制限する」といってもスプライン曲線のように何か特別な関数を用意する必要はありません。 \(H^{1}\) の関数と \(C^{0}\) の関数は同じものを指すと言っても過言ではありませんので、普通の有限要素法(\(C^{0}\) 連続な内挿関数を使った有限要素法)とは非常に相性が良い方法なのです。
4回に渡って解説してきましたノンパラメトリック最適化の難しさは、まとめると次の2点になります。
- ノンパラメトリック最適化は、数学的には関数の最適化で、実際上も非常に多くの設計変数を同時に求める必要がある。
- ノンパラメトリック最適化の過程では、求めるべき関数に凹凸が現れて滑らかさが失われるのを防ぐため、何らかの平滑化を必要とする。
\(H^{1}\) 勾配法はこれら2つの点を同時に解決する最適化手法になっているのです。
*****
次回から数回に分けて \(H^{1}\) 勾配法が具体的にどのような方法なのか解説していきます。
まず次回は、形状最適化の \(H^{1}\) 勾配法である「力法」について、その歴史的な背景も交えて解説していきます。
★ご意見・ご感想はこちらへ★
![]() https://www.quint.co.jp/cgi-bin/qrepo-impr.cgi
https://www.quint.co.jp/cgi-bin/qrepo-impr.cgi
