SOLIDWORKSアドイン構造最適設計ソフトウェア
HiramekiWorks

形状表現にレベルセット関数を用いた最新のトポロジー最適化手法です。
中間密度（グレースケール）問題が生じないため、与えられた体積制約をほぼ正確に満足する、クリアな最適構造が得られます。 また、得られる最適形状の複雑さも調整することができ、 より設計者向けの構造最適化手法 です。

　 　

【特徴1】 目標の体積・質量を精度よく満足！

物体と空間の境界を認識しながら最適化をおこなうため、設定した体積や質量とほぼぴったり合った最適化結果を得ることができます。 従来のトポロジー最適化（SIMP法）のような“しきい値”の調整は必要ありません。

　

【特徴2】 最適化結果形状の複雑さをコントロール可能

計算時のパラメータにより、得られる最適化結果形状の複雑さ（かたまり度合い）を調整することができます。

【特徴3】 メッシュサイズ依存性が低い

メッシュサイズに関係なく同様の最適化結果を得ることができます。
※最適化結果の構造を表せないような粗いメッシュを用ると、収束性が悪化し適切な結果が得られない場合があります。

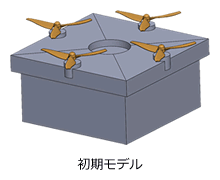
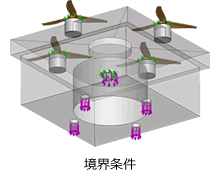
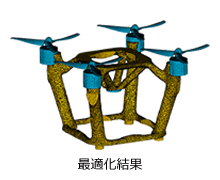
◎解析事例◎ドローン骨格のトポロジー最適化

詳細はこちら HiramekiWorks 事例5

従来のトポロジー最適化との違いは？

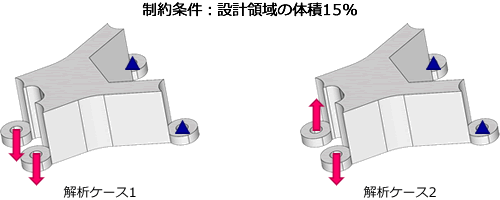
従来のトポロジー最適化（SIMP法）との違いをブラケットの事例を使ってご説明いたします。

下図の条件で剛性の高い形状へ最適化いたします。

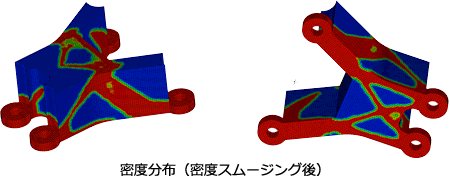
◎最適化結果◎ SIMP法によるトポロジー最適化（従来手法）

最適化結果は密度分布として得られますので、構造を確認するためには “しきい値” を調整する必要があります。 中間密度の領域が広い場合は、しきい値の調整が難しいことがありますが、ある程度粗いメッシュでも計算できますので、比較的短時間で解析できます。

◎最適化結果◎ レベルセット法によるトポロジー最適化

しきい値の調整なしで、指定した条件を満たす明瞭な形状を得ることができます。

このように、2つのトポロジー最適化から用途にあった手法を選んでいただき、ご活用いただけたらと思います。 迷った際には、お気軽にお問い合わせください。

≪ご協力≫
　基礎理論・技術アドバイス
　　東京大学 大学院工学系研究科 数理設計工学研究室・山田 崇恭 先生
　監修（JST A-STEP、SIP）：
　　京都大学 大学院工学研究科 生産システム工学研究室・西脇 眞二 先生

 

▲