満足化トレードオフ法とは?
はじめに
『あれもこれもよくしたい』そんな時にピッタリな最適化、多目的最適化。
多目的最適化の解き方で真っ先に思いつくのは、各目的関数に重みを掛け、その和を新たな目的関数にすることでしょう。
これは「線形加重和法」と呼ばれ、古くから広く利用されています。
しかし、目的関数のオーダーや次元が異なると、その重みの決め方が難しかったり、
重視したい目的関数の重みを大きくしても思ったように改善されなかったり、期待通りの結果を得ることが難しいことがあります。
その問題を解決するために考え出された手法のひとつが「満足化トレードオフ法」です。
AMDESSはこの手法を取り入れ、重みに悩むことなく要望に近い解を求めることができます。
ここでは、「線形加重和法」でうまくいかない問題を「満足化トレードオフ法」で解決する例をご紹介します。
問題 ~ケーキをいい感じに分けたい~
二人を満足させるケーキの分け方は?

100gのケーキをAさん、Bさんの二人で分けることを考えます。
当然、二人ともより多くケーキを食べたいのですが、今日はAさんの誕生日なので、優しいBさんはAさんにちょっと多く切り分けようと思いました。
この “ちょっと多く” の気持ちを反映させた分け方を、最適化で決めたいと思います。
今回の最適化の問題定義は次の通りです。
● 設計変数 ●

決めたい値はAさんBさんのケーキの量。
それぞれ分けられる可能性のあるケーキの量の範囲は、二人とも0g以上100g以下。
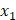 :Aさんのケーキの量(
:Aさんのケーキの量( 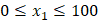 )
)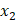 :Bさんのケーキの量(
:Bさんのケーキの量( 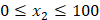 )
)
● 目的関数 ●
AさんもBさんもできるだけ多くケーキを食べたい!
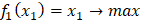 (最大化)
(最大化)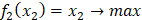 (最大化)
(最大化)
● 制約関数 ●
ケーキの総量は100gなので、AさんBさん二人のケーキを足し合わせた量は100g以下。
線形加重和法では?
まず、線形加重和法を使った最適化で求めてみましょう。
次の様に目的関数を一つにまとめて、F(x) を新たな目的関数とします。
○ 目的関数 ○
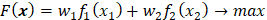 (最大化)
(最大化)
ここで w1 はAさんの重み、w2 はBさんの重みです。
今回はAさんに少し多めに分けたいので、w1=60、w2=50 とします。
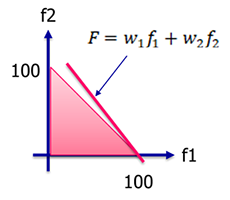
これをグラフに描いて考えると右図の様になります。
グラフの軸は f1 f2 の目的関数で、AさんBさんそれぞれのケーキの量を表しています。赤い直線は上記の新しい目的関数を表しています。 0 ≦ f1 、0 ≦ f2 、f1 + f2 ≦ 100 の制約があるため、直線が動ける範囲は左下の赤い直角二等辺三角形の領域です。
この目的関数を f2 について変形すると、
![]()
となります。
w1、w2 は定数なので、F を大きくするということは、f2 切片を大きくして赤い直線を上に平行移動するということです。赤い三角形の範囲で直線を上に移動させていくと、f1 = 100 で限界になります。
この時の値が最適解となるので、二人のケーキの量はそれぞれ f1=100、f2=0 となります。
ちょっと多く分けるつもりがすべてAさんに渡ってしまい、Bさんの分が無くなってしまいました!
この最適化結果では、さすがに優しいBさんも怒ってしまうでしょう。
満足化トレードオフ法では?
では気を取り直して、満足化トレードオフ法で解いてみましょう。
満足化トレードオフ法は、線形加重和法の重みの代わりに、理想値と目標値(一般には希求水準と呼ばれます)を設定し、理想値と目標値を結んだ直線上から最適解を見つけます。重みは明示的には入力しません。
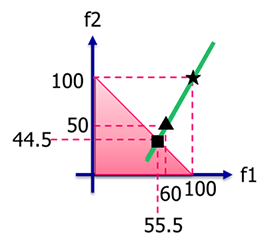
ここでは、理想値は二人とも100g(総取り)、Aさんの目標値を60g、Bさんの目標値を50gと設定します。理想値を★、目標値を▲としてグラフにプロットしたものが右図です。
理想値と目標値を結んだ緑の直線と、パレートフロントすなわち赤い三角形の斜辺の交差する点■が意思を反映したパレート最適解です。
結果として、 f1=55.5、f2=44.5 が得られました。
Aさんにちょっと多く分けられる結果が得られ、これでBさんも大満足ですね。
もっとAさんに多く分けたければ、Aさんの目標値を大きく、Bさんの目標値を小さくすることでそのような解を得ることができます。
まとめ
このように、「線形加重和法」を使うと非常に単純な問題でも思ったような解が得られない場合がありますが、「満足化トレードオフ法」を使うことで良い塩梅の最適解を得ることができます。
思わぬトラブルを避けるためにも、多目的最適化は慎重に行いましょう。