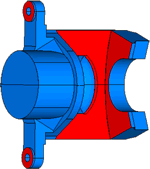
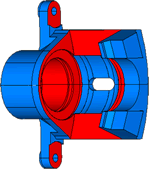
構造最適設計ソフトウェア
OPTISHAPE-TS
事例1 固有振動数を実験計測結果に合わせ込む形状最適化
■概要
固有振動数は機械構造物の振動特性を表す重要な指標の一つです。
この固有振動数が所望の値に一致するような形状を効率良く求めることが、様々な分野の製品開発において求められています。例えば、下記のようなケースが挙げられます。
- 特定の加振周波数において共振を回避する場合．
- 実験値と一致する固有振動数を持つ有限要素モデルを構築する場合． 等...
ここでは、自動車ブレーキ部品において多数の固有振動数を一致させるべく、
OPTISHAPE-TS のノンパラメトリック形状最適化機能を適用した解析例をご紹介します。
■解析モデル
ブレーキキャリパー
- 寸法 ： 約160×135×85 （mm）
- 要素 ： 四面体二次要素
- 要素数 ： 15,922
- 節点数 ： 29,352
- 固有振動解析での拘束条件 ： 無し
- 固有振動解析ソルバー ： ブロックランチョス法
■最適化条件
7次から21次の固有振動モードを対象として、それらの固有振動数を目標値に一致させながら、 体積は変化させないように、以下の条件を設定。
- 最適化手法 ： ノンパラメトリック形状最適化
- 目的関数 ： 体積（ダミー）*1
- 制約関数 ： 7次から20次モードの固有振動数（詳細は下表参照）
| モード次数 | 初期値[Hz] | 制約値[Hz] | モード次数 | 初期値[Hz] | 制約値[Hz] |
|---|---|---|---|---|---|
| 7 | 2475 | 2600 | 14 | 7740 | 8000 |
| 8 | 2636 | 2700 | 15 | 7934 | 8500 |
| 9 | 5029 | 4800 | 16 | 9075 | 9000 |
| 10 | 5501 | 5000 | 17 | 9915 | 10000 |
| 11 | 6021 | 6000 | 18 | 9969 | 10500 |
| 12 | 7123 | 6500 | 19 | 11095 | 11000 |
| 13 | 7199 | 7000 | 20 | 11882 | 11500 |
*1 OPTISHAPE-TS では、少なくとも一つの目的関数を設定する必要があります。
ここでは、体積を変化させないようにするため、体積を目的/制約関数の両方に設定しています。
最適化の過程では制約関数が優先されるため、体積の最小化は実行されません。
形状拘束条件
下図の赤色で示される部位は、最適化の過程で変化しないよう設定。
■結果
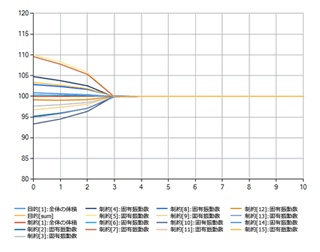誤差0.01%以内の精度で、各固有値及び体積がそれぞれの制約値と一致する結果形状が得られました。
※最適化繰返し回数 ： 10回
（1回の最適化計算につき固有振動解析28回）
※右グラフ参照：目的/制約関数 推移グラフ（クリックで大きく表示します）
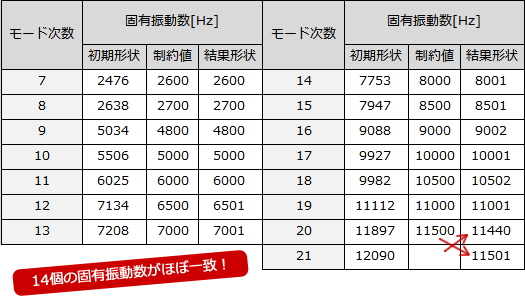
■考察
初期形状と結果形状を比較すると、最大約2割の固有値の差があるにも関わらず、形状の変化は比較的穏やかです。
従来のパラメトリック最適化では、適切な設計パラメータを設定しないと非現実的な形状に陥ったり、目標の固有値に到達しない場合があります。
それに対して、 ノンパラメトリック形状最適化 では、設計パラメータの設定作業無しで表面形状を自由に変化させることで、目標の固有値に到達する現実的な形状を求めることができます。
OPTISHAPE-TS のノンパラメトリック形状最適化は、平滑化勾配法（力法）に基づくアルゴリズムを採用し、多数の制約条件を効率良く取り扱うことが可能です。 この解析例でも、収束過程における目的・制約関数の推移を見ると、最適化が良好に進行した様子が分かります。
また、今回は固有値の制御を初期形状比指定で行いましたが、絶対値での指定や、その他、 固有振動モードの節位置制御や周波数応答等を組み合わせた解析も行うことができます。
お問い合わせ
気になる点やご不明な点等、お気軽にお問い合わせください。
株式会社くいんと 営業本部 Tel 042(362)3884
