Total Solution for Structural Optimization
OPTISHAPE-TS
case study 01 : The Shape Optimization of A Car Brake Part
Outline
Natural Frequency is one of the important indicators to express the vibration characteristic of the machine structure.
In the development of various products, it is demanded to find the shape whose natural frequency accords with the desired value efficiently.
For example, ...
- The case that it evades resonance at specific frequency.
- The case to make the FEM model which has the natural frequency same as the experimental value, etc.
This is an example of the shape optimization to synchronize a lot of natural frequencies of car brakes.
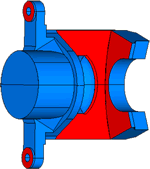
Analysis Model
Car Brake Part
- Scale : About 160*135*85 [mm]
- Element Type : Second-Order Tetrahedral Element
- Number of Elements : 15,922
- Number of Nodes : 29,352
- Constraint Condition in Frequency Response Analysis Solver : none
- Frequency Response Analysis Solver : Block Lanczos Solver
Optimization Condition
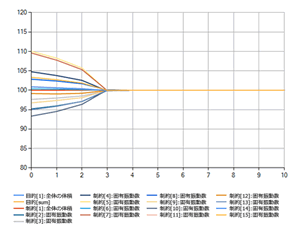
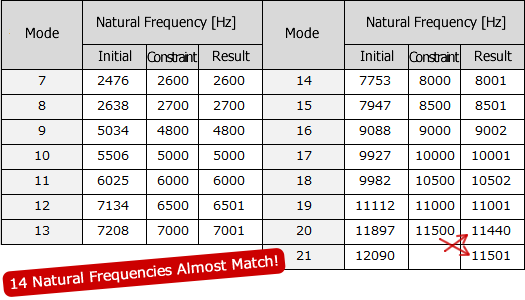
For the 7th to the 21th eigenmodes, OPTISHAPE-TS changes the shape and makes those natural frequencies agree with the target values in the following conditions as keeping the initial volume.
- Optimization Method : Nonparametric Shape Optimization
- Object : Volume (Dummy) *1
- Constraint : as follows
| Eigenvalue Mode |
Initial Value [Hz] |
Constraint Value [Hz] |
Eigenvalue Mode |
Initial Value [Hz] |
Constraint Value [Hz] |
|---|---|---|---|---|---|
| 7 | 2475 | 2600 | 14 | 7740 | 8000 |
| 8 | 2636 | 2700 | 15 | 7934 | 8500 |
| 9 | 5029 | 4800 | 16 | 9075 | 9000 |
| 10 | 5501 | 5000 | 17 | 9915 | 10000 |
| 11 | 6021 | 6000 | 18 | 9969 | 10500 |
| 12 | 7123 | 6500 | 19 | 11095 | 11000 |
| 13 | 7199 | 7000 | 20 | 11882 | 11500 |
* It is necessary for OPTISHAPE-TS to set at least one objective function. Here, it is set a volume in both objective/constraint functions not to change a volume. The minimization of the volume isn't carried out because constraint function is given priority to, in the process of the optimization.
Shape Constraint : The red part of the shape below doesn't change.
Result
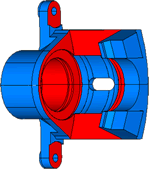
It got the result shape which each eigenvalue and the volume agreed with each specified value. (Precision : Error of 0.001% or less)
- Time : 23 min
- The optimization repetition : 10 times
[ Natural Frequency Analysis : 28 times a step ] - OS ： Red Hat Linux
- CPU ： Core2Quad 2.66GHz
- Memory : 1,200[MB]
Comment
Compare the initial shape and result shape, the cange of shape is comparatively calm though the eigenvalue is different about 20% at the maximum.
In the existing software of the parametric optimization, there is the case that result shape is unrealistic, or doesn't reach the targeted eigenvalue.
However, Nonparametric Shape Optimization changes surface shape freely without setting design parameters, so it can get the realistic shape which eigenvalue satisfies the demand..
Nonparametric Shape Optimization of OPTISHAPE-TS, adopts algorithm based on Smoothing Gradient Method (Traction Method) and can deal with a lot of limitation conditions efficiently. In this case study, you can see the optimization is efficiently going well by the change of values of objective/constraint functions while the convergence.
And, in this case ,it set control of the eigenvalue by initial shape ratio appointment, but can set it by modulus appointment or more, too.
